
£Ø±¾ĢāĀś·Ö12·Ö£¬Ć抔ĢāĀś·Öø÷4·Ö£©ŅŃÖŖĘ½ĆęÖ±½Ē×ų±źĻµxOy£ØČēĶ¼1£©£¬Ņ»“ĪŗÆŹż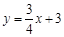 µÄĶ¼ ĻńÓėyÖį½»ÓŚµćA£¬µćMŌŚÕż±ČĄżŗÆŹż
µÄĶ¼ ĻńÓėyÖį½»ÓŚµćA£¬µćMŌŚÕż±ČĄżŗÆŹż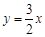 µÄĶ¼ĻńÉĻ£¬ĒŅMO£½MA£®¶ž“ĪŗÆŹży£½x2£«bx£«cµÄĶ¼Ļń¾¹żµćA”¢M£®
µÄĶ¼ĻńÉĻ£¬ĒŅMO£½MA£®¶ž“ĪŗÆŹży£½x2£«bx£«cµÄĶ¼Ļń¾¹żµćA”¢M£®
£Ø1£©ĒóĻ߶ĪAMµÄ³¤£»
£Ø2£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø3£©Čē¹ūµćBŌŚyÖįÉĻ£¬ĒŅĪ»ÓŚµćAĻĀ·½£¬µćCŌŚÉĻŹö¶ž“ĪŗÆŹżµÄĶ¼ĻńÉĻ£¬µćDŌŚŅ»“ĪŗÆŹż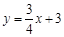 µÄĶ¼ĻńÉĻ£¬ĒŅĖıߊĪABCDŹĒĮāŠĪ£¬ĒóµćCµÄ×ų±ź£®
µÄĶ¼ĻńÉĻ£¬ĒŅĖıߊĪABCDŹĒĮāŠĪ£¬ĒóµćCµÄ×ų±ź£®

(±¾ĢāĀś·Ö12·Ö£¬Ć抔ĢāĀś·Öø÷4·Ö)
[½ā] (1) øł¾ŻĮ½µćÖ®¼ä¾ąĄė¹«Ź½£¬ÉčM(a, 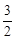 a)£¬ÓÉ|
MO |=| MA |, ½āµĆ£ŗa=1£¬ŌņM(1,
a)£¬ÓÉ|
MO |=| MA |, ½āµĆ£ŗa=1£¬ŌņM(1, 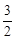 ),
),
¼“AM= ”£
ӣ
(2) ”ß A(0, 3)£¬”ą c=3£¬½«µćM“śČėy=x2+bx+3£¬½āµĆ£ŗb= - £¬¼“£ŗy=x2-
£¬¼“£ŗy=x2- x+3”£
x+3ӣ
(3) C(2, 2) (øł¾ŻŅŌAC”¢BDĪŖ¶Ō½ĒĻßµÄĮāŠĪ)”£×¢Ņā£ŗA”¢B”¢C”¢DŹĒ°“Ė³ŠņµÄ”£
[½ā] ÉčB(0,
m) (m<3)£¬C(n,
n2- n+3)£¬D(n,
n+3)£¬D(n,
 n+3)£¬
n+3)£¬
| AB |=3-m£¬| DC |=yD-yC= n+3-(n2-
n+3-(n2- n+3)=
n+3)= n-n2£¬
n-n2£¬
| AD |= =
= n£¬
n£¬
| AB |=| DC |Þ3-m= n-n2”j£¬|
AB |=| AD |Þ3-m=
n-n2”j£¬|
AB |=| AD |Þ3-m= n”k”£
n”k”£
½āj£¬k£¬µĆn1=0(ÉįČ„)£¬»ņÕßn2=2£¬½«n=2“śČėC(n,
n2- n+3)£¬µĆC(2, 2)”£
n+3)£¬µĆC(2, 2)”£
”¾½āĪö”æĀŌ



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
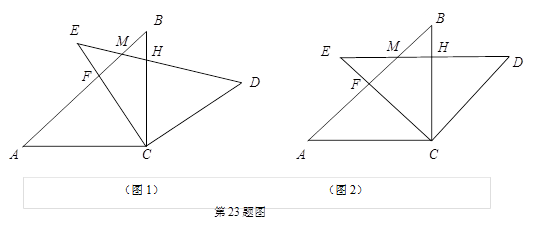
£Ø±¾ĢāĀś·Ö12·Ö£¬Ć抔ĢāĀś·Öø÷6·Ö£©ČēĶ¼£Ø1£©£¬ŌŚ”÷ABCŗĶ”÷EDCÖŠ£¬AC£½CE£½CB£½CD£¬”ĻACB£½”ĻECD£½![]() £¬ABÓėCE½»ÓŚF£¬EDÓėAB”¢BC·Ö±š½»ÓŚM”¢H£®
£¬ABÓėCE½»ÓŚF£¬EDÓėAB”¢BC·Ö±š½»ÓŚM”¢H£®
(1)ĒóÖ¤:CF£½CH£»
(2)ČēĶ¼(2)£¬”÷ABC²»¶Æ£¬½«”÷EDCČʵćCŠż×Ŗµ½”ĻBCE=![]() Ź±£¬ŹŌÅŠ¶ĻĖıߊĪACDMŹĒŹ²Ć“ĖıߊĪ£æ²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
Ź±£¬ŹŌÅŠ¶ĻĖıߊĪACDMŹĒŹ²Ć“ĖıߊĪ£æ²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ŃŲyÖįĻņĻĀĘ½ŅĘ3øöµ„Ī»³¤¶ČŗóĒ”ŗĆ¾¹żB(-3£¬0)¼°yÖįÉĻµÄCµć£®ČōÅ×ĪļĻß
ŃŲyÖįĻņĻĀĘ½ŅĘ3øöµ„Ī»³¤¶ČŗóĒ”ŗĆ¾¹żB(-3£¬0)¼°yÖįÉĻµÄCµć£®ČōÅ×ĪļĻß Óė
Óė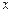 Öį½»ÓŚA£¬BĮ½µć£ØµćAŌŚµćBµÄÓŅ²ą£©£¬ĒŅ¾¹żµćC£¬£Ø1£©ĒóÖ±Ļß
Öį½»ÓŚA£¬BĮ½µć£ØµćAŌŚµćBµÄÓŅ²ą£©£¬ĒŅ¾¹żµćC£¬£Ø1£©ĒóÖ±Ļß ¼°Å×ĪļĻߵĽāĪöŹ½£»£Ø2£©ÉčÅ×ĪļĻߵĶ„µćĪŖ
¼°Å×ĪļĻߵĽāĪöŹ½£»£Ø2£©ÉčÅ×ĪļĻߵĶ„µćĪŖ £¬µć
£¬µć ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬ĒŅ
ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬ĒŅ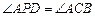 £¬Ēóµć
£¬Ēóµć µÄ×ų±ź£»
µÄ×ų±ź£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2011Äź³õÖŠ±ĻŅµÉżŃ§æ¼ŹŌ£Ø¹ć¶«ÉīŪŚ¾ķ£©ŹżŃ§ ĢāŠĶ£ŗ½ā“šĢā
£Ø±¾ĢāĀś·Ö12·Ö£¬Ć抔ĢāĀś·Öø÷6·Ö£©ČēĶ¼£¬ŌŚĢŻŠĪABCDÖŠ£¬AD//BC£¬AB£½DC£¬¹żµćD×÷DE”ĶBC£¬“¹×ćĪŖE£¬²¢ŃÓ³¤DEÖĮF£¬Ź¹EF£½DE£®ĮŖ½įBF”¢CD”¢AC£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪABFCŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©Čē ¹ūDE2£½BE”¤CE£¬ĒóÖ¤ĖıߊĪABFCŹĒ¾ŲŠĪ£®
¹ūDE2£½BE”¤CE£¬ĒóÖ¤ĖıߊĪABFCŹĒ¾ŲŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2010Äźøß¼¶ÖŠµČѧŠ£ÕŠÉśČ«¹śĶ³Ņ»æ¼ŹŌŹżŃ§¾ķ£ØŌĘÄĻĒś¾ø£© ĢāŠĶ£ŗ½ā“šĢā
£Ø±¾ĢāĀś·Ö12·Ö£¬Ć抔Ģā6·Ö£©
(1) ŌŚČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĻČ»³ö”÷OAB ¹ŲÓŚyÖį¶Ō³ĘµÄĶ¼ŠĪ£¬ŌŁ»³ö”÷OABČʵćOŠż×Ŗ180”ćŗóµĆµ½µÄĶ¼ŠĪ£®
£Ø2£©ĻČŌĶĮŗó×÷“š£ŗĪŅĆĒŅŃ¾ÖŖµĄ£¬øł¾Ż¼øŗĪĶ¼ŠĪµÄĆ껿 ¹ŲĻµæÉŅŌĖµĆ÷ĶźČ«Ę½·½¹«Ź½£¬Źµ¼ŹÉĻ»¹ÓŠŅ»Š©µČŹ½Ņ²æÉŅŌÓĆÕāÖÖ·½Ź½¼ÓŅŌĖµĆ÷£¬ĄżČē£ŗ(2a +b)( a +b) =" 2a2" +3ab +b2£¬¾ĶæÉŅŌÓĆĶ¼22£1µÄĆ껿¹ŲĻµĄ“ĖµĆ÷£®


¢Ł øł¾ŻĶ¼22£2Š“³öŅ»øöµČŹ½ £»
¢Ś ŅŃÖŖµČŹ½£ŗ(x +p£©(x +q£©="x2" + (p +q) x + pq£¬ĒėÄć»³öŅ»øöĻąÓ¦µÄ¼øŗĪĶ¼ŠĪ¼ÓŅŌĖµĆ÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2011Äź³õÖŠ±ĻŅµÉżŃ§æ¼ŹŌ£ØĢģ½ņ¾ķ£©ŹżŃ§ ĢāŠĶ£ŗ½ā“šĢā
£Ø±¾ĢāĀś·Ö12·Ö£¬Ć抔ĢāĀś·Öø÷4·Ö£©ŅŃÖŖĘ½ĆęÖ±½Ē×ų±źĻµxOy£ØČēĶ¼1£©£¬Ņ»“ĪŗÆŹż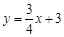 µÄĶ¼ ĻńÓėyÖį½»ÓŚµćA£¬µćMŌŚÕż±ČĄżŗÆŹż
µÄĶ¼ ĻńÓėyÖį½»ÓŚµćA£¬µćMŌŚÕż±ČĄżŗÆŹż µÄĶ¼ĻńÉĻ£¬ĒŅMO£½MA£®¶ž“ĪŗÆŹży£½x2£«bx£«cµÄĶ¼Ļń¾¹żµćA”¢M£®
µÄĶ¼ĻńÉĻ£¬ĒŅMO£½MA£®¶ž“ĪŗÆŹży£½x2£«bx£«cµÄĶ¼Ļń¾¹żµćA”¢M£®
£Ø1£©ĒóĻ߶ĪAMµÄ³¤£»
£Ø2£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø3£©Čē¹ūµćBŌŚyÖįÉĻ£¬ĒŅĪ»ÓŚµćAĻĀ·½£¬µćCŌŚÉĻŹö¶ž“ĪŗÆŹżµÄĶ¼ĻńÉĻ£¬µćDŌŚŅ»“ĪŗÆŹż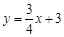 µÄĶ¼ĻńÉĻ£¬ĒŅĖıߊĪABCDŹĒĮāŠĪ£¬ĒóµćCµÄ×ų±ź£®
µÄĶ¼ĻńÉĻ£¬ĒŅĖıߊĪABCDŹĒĮāŠĪ£¬ĒóµćCµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com