
【题目】已知A、B两地相距50单位长度。小李从A地出发去B地,以每分钟2单位长度的速度行进,第一次他向左1单位长度,第二次他向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度,……,按此规律行进,如果A地在数轴上表示的数为-16.
(1)B地在数轴上表示的数为________________。
(2)若B地在原点的右侧,经过第八次进行后,小李到达点P,此时点P与点B相距_____________单位长度,八次运动完成后一共经过__________分钟。
(3)若经过n次(n为正整数)行进后,小李到达点Q,在数轴上点Q表示的数如何表示?(直接写出结果)
【答案】(1)-66或34;(2)46,18;(3)n为奇数时,![]() ;n为偶数时,
;n为偶数时,![]()
【解析】
(1)由题意可得点B位于点A的左侧或右侧,AB两地相距50单位长度,A地在数轴上表示的数为-16,可以得到B地在数轴上表示的数;
(2)根据题意可以发现奇数次运动和偶数次运动是有一定规律的,从而可以得到第八次行进后小李到达点P,此时点P与点B相距几个单位长度和八次运动完成后一共经过了几分;
(3)根据题意可以发现奇数次运动和偶数次运动是有一定规律的,从而可以写出n为偶数和奇数时,在数轴上点Q表示的数是什么.
(1)∵AB两地相距50单位长度,A地在数轴上表示的数为16,
∴点B表示的数为:1650=66或16+50=34,
即B地在数轴上表示的数是66或34;
(2)由题意可得,
第一次运动到点:161,
第二次为:161+2=16+1,
第三次为:16+13=162,
第四次为:162+4=16+2,
由上可得,第奇数次运动到点16![]() ,第偶数次运动到点:16+
,第偶数次运动到点:16+![]() ,
,
∴第八次运动到点P为:16+![]() =16+4=12,
=16+4=12,
∵B地在原点的右侧,
∴点B表示的数为:34,
∴点P与点B相距的单位长度为:34(12)=46,
∴八次运动完成后经过的时间为:(1+2+3+4+5+6+7+8)÷2=36÷2=18(分钟),
即B地在原点的右侧,经过第八次行进后小李到达点P,此时点P与点B相距46个单位长度,八次运动完成后一共经过了18分钟;
(3)由题意可得,
第一次运动到点:161,
第二次为:161+2=16+1,
第三次为:16+13=162,
第四次为:162+4=16+2,
由上可得,第奇数次运动到点16![]() ,第偶数次运动到点:16+
,第偶数次运动到点:16+![]() ,
,
即当n为奇数时,在数轴上点Q表示的数为:16![]() ;当n为偶数时,在数轴上点Q表示的数为:16+
;当n为偶数时,在数轴上点Q表示的数为:16+![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD//OB,则图中休闲区(阴影部分)的面积是( ) 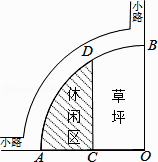
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
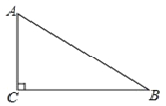
【题目】如图,在 ABC ,C 90,AC<BC,D 为 BC 上一点,且到 A、B 两点的距离相等.
(1)用直尺和圆规,作出点 D 的位置(不写作法,保留作图痕迹);
(2)连结 AD,若 B 36 ,求∠CAD 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
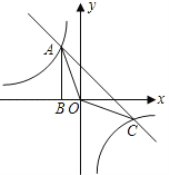
【题目】如图,Rt△ABO的顶点A是双曲线y1=![]() 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com