
【题目】在![]() 中,BD是它的一条对角线,过A、C两点分别作
中,BD是它的一条对角线,过A、C两点分别作![]() ,
,![]() ,E、F为垂足.
,E、F为垂足.
(1)如图,求证:![]() ;
;
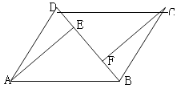
(2)如图,连接AC,设AC、BD交于点O,若![]() .在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
.在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
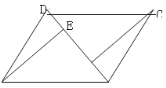
【答案】(1)见解析;(2)OA、OC、EF.
【解析】
(1)根据平行四边形的AD∥BC,AB∥CD,AD=BC,AB=CD,根据平行线的性质得到∠ADE=∠CBF,由垂直的定义得到∠AEB=∠CFD=90°,根据全等三角形的性质即可得到结论;
(2)根据平行四边形的性质得到AO=CO,根据直角三角形的性质即可得到结论.
(1)证明:∵四边形ABCD是平行四边形
∴![]()
![]()
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中
中
∴![]()
∴![]()
(2)∵四边形ABCD是平行四边形,
∴AO=CO,
∵∠DOC=120°,
∴∠AOE=60°,
∴∠OAE=30°,
∴AO=2OE,
∴OC=2OE,
∵OD=OB,DE=BF,
∴OE=OF,
∴EF=2OE.


科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
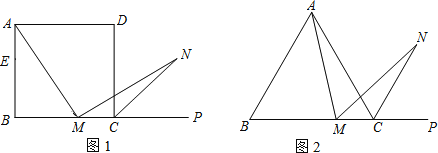
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:在图(1)(2)所示抛物线中,抛物线与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() ,点
,点![]() 是抛物线的顶点,过
是抛物线的顶点,过![]() 平行于
平行于![]() 轴的直线是它的对称轴,点
轴的直线是它的对称轴,点![]() 在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:
在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:

(1)在图①中作出点![]() ,使线段
,使线段![]() 最小;
最小;
(2)在图②中作出点![]() ,使线段
,使线段![]() 最大.
最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=ax2-2ax+c经过点C(1,2),与x轴交于A(-1,0)、B两点
(1) 求抛物线C的解析式
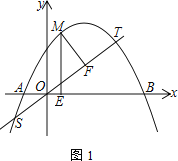
(2) 如图1,直线![]() 交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
(3) 如图2,平移抛物线C的顶点到原点得抛物线C1,直线l:y=kx-2k-4交抛物线C1于P、Q两点,在抛物线C1上存在一个定点D,使∠PDQ=90°,求点D的坐标
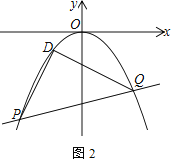
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上,点A表示a, 点B表示b, 点C表示c,b是最大的负整数,且a,c满足![]()
![]()
![]() ________,
________,![]() _________,
_________,![]() _____________
_____________
![]() 若将数轴折叠,使得
若将数轴折叠,使得![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数____________表示的点重合;
与数____________表示的点重合;
![]() 点
点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设![]() 秒钟过后,
秒钟过后,
①请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
②探究:若点![]() 向右运动,点
向右运动,点![]() 向左运动,速度保持不变,
向左运动,速度保持不变,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“一起阅读,共同成长”课外读书周活动,活动后期随机调查了八年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
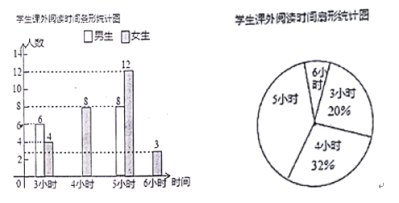
(1)本次调查的学生总数为______人,在扇形统计图中,课外阅读时间为5小时的扇形圆心角度数是______;
(2)请你补全条形统计图;
(3)若全校八年级共有学生![]() 人,估计八年级一周课外阅读时间至少为
人,估计八年级一周课外阅读时间至少为![]() 小时的学生有多少人?
小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
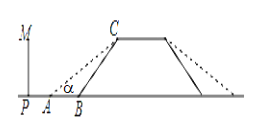
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某公园准备修建一块长方形草坪,长为a米,宽为b米.并在草坪上修建如图所示的十字路,
已知十字路宽2米.
(1)用含a、b的代数式表示修建的十字路的面积.
(2)若a=30,b=20,求草坪(阴影部分)的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com