
【题目】如图①,在平面直角坐标系中,点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,
轴上,![]() 轴,
轴,![]() .点
.点![]() 从
从![]() 点出发,以1cm/s的速度沿边
点出发,以1cm/s的速度沿边![]() 匀速运动,点
匀速运动,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 匀速运动.点
匀速运动.点![]() 与点
与点![]() 同时出发,其中一点到达终点,另一点也随之停止运动.设点
同时出发,其中一点到达终点,另一点也随之停止运动.设点![]() 运动的时间为
运动的时间为![]() (s),
(s),![]() 的面积为
的面积为![]() (cm2),己知
(cm2),己知![]() 与
与![]() 之间的函数关系如图②中的曲线段
之间的函数关系如图②中的曲线段![]() 、线段
、线段![]() 与曲线段
与曲线段![]() .
.


(1)点![]() 的运动速度为 cm/s,点
的运动速度为 cm/s,点![]() 的坐标为 ;
的坐标为 ;
(2)求曲线![]() 段的函数解析式;
段的函数解析式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是四边形
的面积是四边形![]() 的面积的
的面积的![]()
【答案】(1)3,B(18,9)(2)s=-![]() (3)t=2
(3)t=2![]() 或
或![]()
【解析】
(1)结合函数图象得出当3秒时,BP=3,此时△BPQ的面积为13.5cm2,进而求出AO为9cm,即可得出Q点的速度,进而求出AB的长即可;
(2)首先得出PB=t,BQ=30-3t,则QM=![]() (30-3t)=18-
(30-3t)=18-![]() t,利用S△PBQ=
t,利用S△PBQ=![]() t(18-
t(18-![]() t)求出即可;
t)求出即可;
(3)首先得出△BPQ的面积,房两种情形分别列出方程即可解决问题.
解:(1)由题意可得出:当3秒时,△BPQ的面积的函数关系式改变,则Q在AO上运动3秒,
当3秒时,BP=3,此时△BPQ的面积为13.5cm2,
∴AO为9cm,
∴点Q的运动速度为:9÷3=3(cm/s),
当运动到5秒时,函数关系式改变,则CO=6cm,
∵cosB=![]() ,
,
∴可求出AB=6+12=18(cm),
∴B(18,9);
故答案为:3,(18,9);
(2)如图(1):PB=t,BQ=30-3t,
过点Q作QM⊥AB于点M,
则QM=![]() (30-3t)=18-
(30-3t)=18-![]() t,
t,
∴S△PBQ=![]() t(18-
t(18-![]() t)=-
t)=-![]() t2+9t(5≤t≤10),
t2+9t(5≤t≤10),
即曲线FG段的函数解析式为:S=-![]() t2+9t;
t2+9t;
(3)∵S梯形OABC=![]() (6+18)×9=108,
(6+18)×9=108,
∴S=![]() ×108=12,
×108=12,
当0<t<3时,S=![]() t2,S=12时,t=2
t2,S=12时,t=2![]() 或-2
或-2![]() (舍弃),
(舍弃),
当5<t<10时,12=-![]() t2+9t;
t2+9t;
解得t=![]() 或
或![]() (舍弃),
(舍弃),
综上所述:t=![]() 或
或![]() ,△BPQ的面积是四边形OABC的面积的
,△BPQ的面积是四边形OABC的面积的![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销量,增加盈利,商场决定采取适当的降价措施,经调查发现,在一定范围内,衬衫的单价每降
元,为了扩大销量,增加盈利,商场决定采取适当的降价措施,经调查发现,在一定范围内,衬衫的单价每降![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件,如果商场通过销售这批衬衫每天盈利
件,如果商场通过销售这批衬衫每天盈利![]() 元,衬衫的单价下降
元,衬衫的单价下降![]() 元.
元.
![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 写出自变量
写出自变量![]() 的取值范围;
的取值范围;
![]() 若该品牌衬衫单价每件降
若该品牌衬衫单价每件降![]() 元,则该商场每天可盈利多少元?
元,则该商场每天可盈利多少元?
![]() 若该商场每天要盈利
若该商场每天要盈利![]() 元,则该品牌衬衫每件应降多少元?
元,则该品牌衬衫每件应降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪在用描点法画二次函数y=ax2+bx+c![]() 的图象时,列出下面的表格:
的图象时,列出下面的表格:
x | … | -5 | -4 | -3 | -2 | -1 | … |
y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
根据表格提供的信息,下列说法错误的是( ).
A. 该抛物线的对称轴是直线x=-2![]()
B. b2-4ac>0![]()
C. 该抛物线与y![]() 轴的交点坐标为(0,-3.5)
轴的交点坐标为(0,-3.5)
D. 若(0.5,y1)![]() 是该抛物线上一点.则y1<-2.5
是该抛物线上一点.则y1<-2.5![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点(
经过点(![]() 1,0),对称轴为
1,0),对称轴为![]() .则下列结论:①
.则下列结论:①![]() ;②
;② ![]() ;③
;③![]() ; ④
; ④![]() .其中所有正确的结论是( )
.其中所有正确的结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() 分别是梯形
分别是梯形![]() 各边
各边![]() 、
、![]() 、
、![]() 、
、![]() 的中点.
的中点.
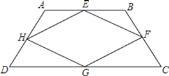
![]() 求证:四边形
求证:四边形![]() 平行四边形;
平行四边形;
![]() 当梯形
当梯形![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是菱形;
是菱形;
![]() 在
在![]() 的条件下,梯形
的条件下,梯形![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线![]() 图象的一部分,已知抛物线的对称轴是
图象的一部分,已知抛物线的对称轴是![]() ,与
,与![]() 轴的一个交点是
轴的一个交点是![]() ,有下列结论:
,有下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;
;
⑤点![]() ,
,![]() 都在抛物线上,则有
都在抛物线上,则有![]() .
.
其中正确的是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com