
【题目】如图,抛物线y= ![]() x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).
x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).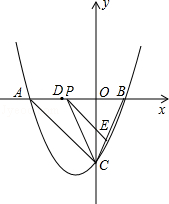
(1)求该抛物线的解析式.
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
【答案】
(1)
解:把点C(0,﹣4),B(2,0)分别代入y= ![]() x2+bx+c中,
x2+bx+c中,
得 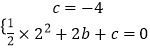 ,
,
解得 ![]()
∴该抛物线的解析式为y= ![]() x2+x﹣4
x2+x﹣4
(2)
解:令y=0,即 ![]() x2+x﹣4=0,解得x1=﹣4,x2=2,
x2+x﹣4=0,解得x1=﹣4,x2=2,
∴A(﹣4,0),S△ABC= ![]() ABOC=12.
ABOC=12.
设P点坐标为(x,0),则PB=2﹣x.
∵PE∥AC,
∴∠BPE=∠BAC,∠BEP=∠BCA,
∴△PBE∽△BAC,
∴ ![]() ,即
,即 ![]() ,
,
化简得:S△PBE= ![]() (2﹣x)2.
(2﹣x)2.
S△PCE=S△PCB﹣S△PBE= ![]() PBOC﹣S△PBE=
PBOC﹣S△PBE= ![]() ×(2﹣x)×4﹣
×(2﹣x)×4﹣ ![]() (2﹣x)2
(2﹣x)2
= ![]() x2﹣
x2﹣ ![]() x+
x+ ![]()
=﹣ ![]() (x+1)2+3
(x+1)2+3
∴当x=﹣1时,S△PCE的最大值为3
(3)
解:△OMD为等腰三角形,可能有三种情形:
(I)当DM=DO时,如答图①所示.
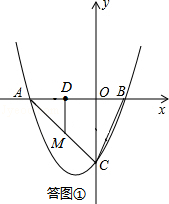
DO=DM=DA=2,
∴∠OAC=∠AMD=45°,
∴∠ADM=90°,
∴M点的坐标为(﹣2,﹣2);
(II)当MD=MO时,如答图②所示.
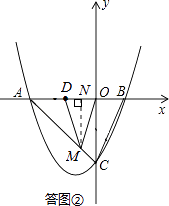
过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3,
∴M点的坐标为(﹣1,﹣3);
(III)当OD=OM时,
∵△OAC为等腰直角三角形,
∴点O到AC的距离为 ![]() ×4=
×4= ![]() ,即AC上的点与点O之间的最小距离为
,即AC上的点与点O之间的最小距离为 ![]() .
.
∵ ![]() >2,∴OD=OM的情况不存在.
>2,∴OD=OM的情况不存在.
综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3)
【解析】(1)利用待定系数法求出抛物线的解析式;(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值;(3)△OMD为等腰三角形,可能有三种情形,需要分类讨论.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 ![]() 的长为( )
的长为( ) 
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为“湘一点”.
(1)求函数y=![]() x-3的图象上所有“湘一点”的坐标;
x-3的图象上所有“湘一点”的坐标;
(2)若直线y=mx+m(m为常数)与直线y=x-2的交点为“湘一点”,试求出整数m的值.
(3)若直线y=-x+b、直线y=3、直线y=x+2所围成的平面图形中(不含边界)共有6个“湘一点”,试求出常数b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共70个,请回答下列问题:

(1)本周“百姓热线”共接到热线电话多少个?
(2)有关道路交通问题的电话多少个?
(3)计算其他各类电话的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(-P)2·(-P)3=_________
(2)若xm=x2×(-x)4,则m=__________
(3)若a3·am=a9,则m=__________
(4)计算22012-22013=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作一次函数表达式中的k,将B转盘指针指向的数字记作一次函数表达式中的b.
(1)请用列表或画树状图的方法写出所有的可能;
(2)求一次函数y=kx+b的图象经过一、二、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )

A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com