
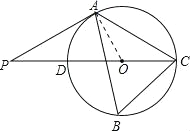
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+![]() ,BC=2
,BC=2![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)详见解析;(2)⊙O的半径为![]() .
.
【解析】
试题分析:(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,再由AP=AC得出∠P=30°,继而由∠OAP=∠AOC﹣∠P,可得出OA⊥PA,从而得出结论;
(2)过点C作CE⊥AB于点E.在Rt△BCE中,∠B=60°,BC=2![]() ,于是得到BE=
,于是得到BE=![]() BC=
BC=![]() ,CE=3,根据勾股定理得到AC=
,CE=3,根据勾股定理得到AC=![]() =5,于是得到AP=AC=5.解直角三角形即可得到结论.
=5,于是得到AP=AC=5.解直角三角形即可得到结论.
试题解析:(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:过点C作CE⊥AB于点E.
在Rt△BCE中,∠B=60°,BC=2![]() ,
,
∴BE=![]() BC=
BC=![]() ,CE=3,
,CE=3,
∵AB=4+![]() ,
,
∴AE=AB﹣BE=4,
∴在Rt△ACE中,AC=![]() =5,
=5,
∴AP=AC=5.
∴在Rt△PAO中,OA=![]() ,
,
∴⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
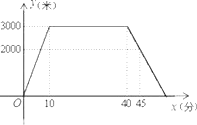
【题目】小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示.请根据图象回答下列问题:
(1)小敏去超市途中的速度是 ;在超市逗留了 ;
(2)小敏几点几分返回到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0. ![]()
(1)求A、B两点的坐标;
(2)点C在数轴上对应的数为x,且x是方程2x+1= ![]() x﹣8的解
x﹣8的解
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若把一次函数y=2x﹣3,向下平移3个单位长度,得到图象解析式是( )
A. y=2x B. y=2x﹣6 C. y=5x﹣3 D. y=﹣x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
①射线 AB 和射线 BA 是同一条射线;②若 AB=BC,则点B为线段AC的中点;③同角的补角相等;④线段AB和线段BA 是同一条线段
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学测试统计成绩,老师发现某题题目有错误,造成该题没有同学答对,于是决定在试卷总分不变的情况下,该题不算分 ,重新统计成绩前后统计量没有发生变化的是
A. 平均数B. 众数C. 中位数D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com