【题目】凸四边形
的四个顶点满足：每一个顶点到其他三个顶点距离之积都相等．则四边形一定是（ ）
A. 正方形 B. 菱形 C. 等腰梯形 D. 矩形
【答案】D
【解析】
根据每一个顶点到其他三个顶点距离之积都相等，可得S=ABADAC…①，S=BABDBC…②，S=CACBCD…③，S=DADBDC…④，然后由②、④得ABBC=ADCD（1），由①、③得BCCD=ABAD（2），再由（1）除以（2）可得AB=CD，同样的方法可得BC=AD，AC=BD，由此即可判定四边形的形状．
以A点的角度看，S=ABADAC…①
以B点的角度看，S=BABDBC…②
以C点的角度看，S=CACBCD…③
以D点的角度看，S=DADBDC…④
由②、④得ABBC=ADCD…（1）
由①、③得BCCD=ABAD…（2）
由（1）÷（2）得，
，
∴CD2=AB2，即CD=AB，
同理可得：BC=AD，AC=BD，
∴四边形ABCD是矩形，
故选D．
A加金题 系列答案
全优测试卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，AC=BC=4cm，点D是斜边AB的中点，点E从点B出发以1cm/s的速度向点C运动，点F同时从点C出发以一定的速度沿射线CA方向运动，规定：当点E到终点C时停止运动；设运动的时间为x秒，连接DE、DF．
（1）填空：S△ABC= cm2；
（2）当x=1且点F运动的速度也是1cm/s时，求证：DE=DF；
（3）若动点F以3cm/s的速度沿射线CA方向运动；在点E、点F运动过程中，如果有某个时间x，使得△ADF的面积与△BDE的面积存在两倍关系，请你直接写出时间x的值；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将
绕点
按逆时针方向旋转
度，并使各边长变为原来的
倍，得
，即如图①，我们将这种变换记为
．
如图①，对作变换
得，则
________；直线
与直线
所夹的锐角为________度；
如图②，中，
，
，对作变换得，使点
、
、
在同一直线上，且四边形
为矩形，求和的值；
如图③，
，
，
，对作变换得，使点、、
在同一直线上，且四边形
为平行四边形，求和的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰Rt△ABC中，∠BAC＝90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM，下列结论：①AE＝AF；②DF＝DN；③AE＝CN；④△AMD和△DMN的面积相等，其中错误的结论个数是（ ）
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一张长12cm、宽5cm的矩形纸片内，要折出一个菱形．小华同学按照取两组对边中点的方法折出菱形EFGH（见方案一），小丽同学沿矩形的对角线AC折出∠CAE=∠CAD，∠ACF=∠ACB的方法得到菱形AECF（见方案二）．
（1）你能说出小华、小丽所折出的菱形的理由吗？
（2）请你通过计算，比较小华和小丽同学的折法中，哪种菱形面积较大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在等边三角形ABC中，点D是BC的中点，点E、F分别是边AB、AC（含线段AB、AC的端点）上的动点，且∠EDF＝120°，小明和小慧对这个图形展开如下研究：
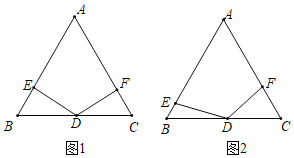
问题初探：（1）如图1，小明发现：当∠DEB＝90°时，BE+CF＝nAB，则n的值为 ；
问题再探：（2）如图2，在点E、F的运动过程中，小慧发现两个有趣的结论：
①DE始终等于DF；②BE与CF的和始终不变；请你选择其中一个结论加以证明．
成果运用:（3）若边长AB＝8，在点E、F的运动过程中，记四边形DEAF的周长为L，L＝DE+EA+AF+FD，则周长L 取最大值和最小值时E点的位置?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则
周长的最小值为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在等腰
中，
，点
为边
上一点（不与点
、点
重合），
，垂足为
，交
于点
.
（1）请猜想
与
之间的数量关系，并证明；
（2）若点为边延长线上一点，，垂足为，交
延长线于点，请在图2中画出图形，并判断（1）中的结论是否成立.若成立，请证明；若不成立，请写出你的猜想并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
