
【题目】已知一次函数y=(3-k)x-2k2+18.
(1)当k为何值时,它的图象经过原点?
(2)当k为何值时,它的图象经过点(0,-2)?
(3)当k为何值时,它的图象平行于直线y=-x?
(4)当k为何值时,y随x增大而减小?
【答案】(1)见解析;(2) k=±![]() ;(3) k=4;(4) k>3.
;(3) k=4;(4) k>3.
【解析】(1) 将点(0,0)代入解析式y=(3-k)x-2k2+18;(2)将点(0,-2)代入解析式y=(3-k)x-2k2+18;(3)由图像平行于直线y=-x,得两个函数的一次项系数相等,即3-k=-1;
(4)y随x的增大而减小,根据一次函数的性质可知,一次项系数小于0.
解:(1)∵一次函数的图像经过原点,
∴点(0,0)在一次函数的图像上,
将点(0,0)代入解析式得:0=-2k2+18,
解得:k=±3.
又∵y=(3-k)x-2k2+18是一次函数,
∴3-k≠0,
∴k≠3.
∴k=-3.
(2)∵图像经过点(0,-2),
∴点(0,-2)满足函数解析式,代入得:-2=-2k2+18,
解得:k=±![]() .
.
(3)∵图像平行于直线y=-x,
∴两个函数的一次项系数相等,即3-k=-1.
解得k=4.
(4)y随x的增大而减小,根据一次函数的性质可知,一次项系数小于0,
即3-k<0,
解得k>3.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3h后安排工人装箱,若每小时装产品150件,未装箱的产品数量(y)是时间(x)的函数,那么这个函数的大致图像只能是( )
A. 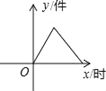 B.
B. 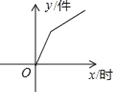 C.
C. 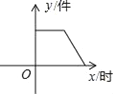 D.
D. 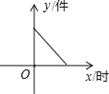
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,且AB= ![]() .点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA. 
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为 ![]() ,直接写出∠BAF的度数.
,直接写出∠BAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A. 20千米/小时 B. 60千米/小时
C. 25千米/小时 D. 75千米小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚与小亮一起玩一种转盘游戏,图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“1”,“2”,“3”表示.固定指针,同时转动两个转盘,任其自由停止. 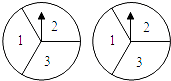
(1)用树状图或者列表法表示所有可能的结果;
(2)求两指针指的数字之和等于4的概率;
(3)若两指针指的数字都是奇数,则小刚获胜;否则,小亮获胜.游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 是正方形
是正方形![]() 的两个顶点,以它的对角线
的两个顶点,以它的对角线![]() 为一边作正方形
为一边作正方形![]() ,以正方形
,以正方形![]() 的对角线
的对角线![]() 为一边作正方形
为一边作正方形![]() ,再以正方形
,再以正方形![]() 的对角线
的对角线![]() 为一边作正方形
为一边作正方形![]() ,…,依次进行下去,则点
,…,依次进行下去,则点![]() 的坐标是( )
的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com