
分析 (1)首先计算乘方、开方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
(2)首先根据非负数的性质,求出a、b的值各是多少;然后化简$\frac{{a}^{2}+2ab+{b}^{2}}{2ab}$÷($\frac{1}{a}$+$\frac{1}{b}$),再把求出的a、b的值代入化简后的算式,求出算式的值是多少即可.
解答 解:(1)$\sqrt{12}$-6tan30°-($\sqrt{15}$-2)0+($\frac{1}{2}$)-2
=2$\sqrt{3}$-6×$\frac{\sqrt{3}}{3}$-1+4
=2$\sqrt{3}$-2$\sqrt{3}$+3
=3
(2)∵|a+2017|+(b-2015)2=0,
∴a+2017=0,b-2015=0,
解得a=-2017,b=2015,
$\frac{{a}^{2}+2ab+{b}^{2}}{2ab}$÷($\frac{1}{a}$+$\frac{1}{b}$)
=$\frac{{(a+b)}^{2}}{2ab}$÷$\frac{a+b}{ab}$
=$\frac{a+b}{2}$
=$\frac{-2017+2015}{2}$
=-1
点评 此题主要考查了分式的化简求值问题,零指数幂、负整数指数幂、特殊角的三角函数值的求法,要熟练掌握,化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
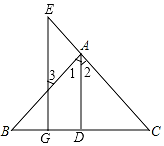 看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
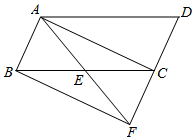 如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F,且AF=AD,连接BF,求证:四边形ABFC是矩形.
如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F,且AF=AD,连接BF,求证:四边形ABFC是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
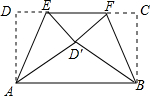 如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为$\frac{8}{3}$.
如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为$\frac{8}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
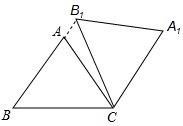 在△ABC中,AB=AC=5,cos∠ABC=$\frac{3}{5}$,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA延长线上(如图).
在△ABC中,AB=AC=5,cos∠ABC=$\frac{3}{5}$,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA延长线上(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
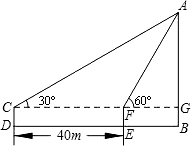 上完《解直角三角形》这章后,一次数学课外活动时,数学兴趣小组的张进、阿芬和晓晨等人在校园里测量如图所示的教学楼的高度AB.
上完《解直角三角形》这章后,一次数学课外活动时,数学兴趣小组的张进、阿芬和晓晨等人在校园里测量如图所示的教学楼的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
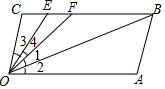 如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.
如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com