
����Ŀ��Ϊ�᳹��������ˮ��ɽ���ǽ�ɽ��ɽ����������мƻ�����ס����������繲7000�����ڳ����̻�����������ÿ��24Ԫ��һ������ÿ��30Ԫ![]() ������ϱ������ס�����������ijɻ��ʷֱ�Ϊ
������ϱ������ס�����������ijɻ��ʷֱ�Ϊ![]() ��
��![]() ��
��
![]() ���������������繲��ȥ180000Ԫ����ס��������������������ꣿ
���������������繲��ȥ180000Ԫ����ס��������������������ꣿ
![]() ��Ҫʹ����������ܳɻ��ʲ�����
��Ҫʹ����������ܳɻ��ʲ�����![]() ��������������������ꣿ
��������������������ꣿ
![]() ��
��![]() �������£�Ӧ���ѡ�����磬ʹ��������ķ�����ͣ��������ͷ��ã�
�������£�Ӧ���ѡ�����磬ʹ��������ķ�����ͣ��������ͷ��ã�
���𰸡�![]() �ס����������������5000��2000����
�ס����������������5000��2000����![]() �������������2800����
�������������2800����![]() ���ٷ���Ϊ
���ٷ���Ϊ![]() Ԫ.
Ԫ.
��������
![]() �з�����⼴�ɣ�
�з�����⼴�ɣ�
![]() �������⣬������������Ĵ�������ڵ�������������
�������⣬������������Ĵ�������ڵ�������������![]() �г�����ʽ��
�г�����ʽ��
![]() ��x��ʾ����������ܷ��ã�����һ�κ���������������Сֵ��
��x��ʾ����������ܷ��ã�����һ�κ���������������Сֵ��
![]() �蹺���������x�꣬������������
�蹺���������x�꣬������������![]() �꣬
�꣬
���������![]()
���![]() ����
����![]()
�𣺼ס����������������5000��2000����
![]() �����������
�����������![]()
���![]()
��������������2800��
![]() �蹺������ķ���ΪW��
�蹺������ķ���ΪW��
��������ã�![]()
![]()
![]() ��x���������С
��x���������С
![]() ��
��![]() ʱ��
ʱ��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B����C��AD��BC������ΪD��AEƽ����BAC����֪��B=65������DAE=20��������C�Ķ�����
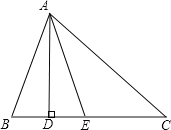
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC������Ϊa��b��c�����������������ж�����ֱ�������ε�����������
A. ��A: ��B: ��C =3��4��5 B. ��A=��B+��C
C. a2=(b+c)(b-c) D. a:b:c =1��2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
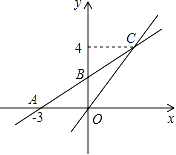
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����x�ύ��ΪA����3��0������y�ύ��ΪB����������������y=![]() x��ͼ���ڵ�C��m��4����
x��ͼ���ڵ�C��m��4����
��1����m��ֵ��һ�κ���y=kx+b�ı���ʽ��
��2���۲캯��ͼ��ֱ��д������x�IJ���ʽ![]() x��kx+b�Ľ⼯��
x��kx+b�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������һ�ű߳�Ϊ4��������ֽƬABCD����PΪ������AD���ϵ�һ�㣨�����A����D�غϣ���������ֽƬ�۵���ʹ��B����P������C����G����PG��DC��H���ۺ�ΪEF������BP��BH�� 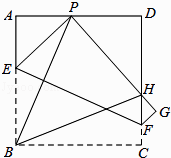
��1����֤����APB=��BPH��
��2������P�ڱ�AD���ƶ�ʱ����PDH���ܳ��Ƿ����仯����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����������ĸ����ۣ���abc=0����a+b+c��0����a��b����4ac��b2��0��������ȷ�Ľ����У� �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OPƽ����BOA��PC��OA��PD��OB������ֱ���C��D�������н����д�����ǣ�������

A. PC=PD B. OC=OD C. OC=OP D. ��CPO=��DPO
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������������֤�����̣�����ÿ�������������д�ò����������ݣ�
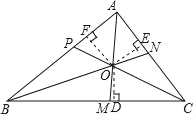
��֪����ͼ��AM��BN��CP����ABC��������ƽ���ߣ�
��֤��AM��BN��CP����һ�㣮
֤������ͼ����AM��BN���ڵ�O������O�ֱ���OD��BC��OF��AB������ֱ�Ϊ��D��E��F��
��O����BAC��ƽ����AM�ϵ�һ���� ����
��OE=OF�� ����
ͬ����OD=OF��
��OD=OE�� ����
��CP����ACB��ƽ������ ����
��O��CP���� ����
��ˣ�AM��BN��CP����һ�㣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com