
 如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$.
如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$. 分析 过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,连AO1,则在Rt△ADO1中,可求得$\sqrt{3}$r,四边形ADO1E的面积等于三角形ADO1的面积的2倍,还可求出扇形O1DE的面积,所求面积等于四边形ADO1E的面积减去扇形O1DE的面积的三倍.
解答  解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,
连结AO1,则Rt△ADO1中,∠O1AD=30°,O1D=r,AD=$\sqrt{3}$r,
∴${S}_{△AD{O}_{1}}=\frac{1}{2}{O}_{1}D•AD=\frac{\sqrt{3}}{2}{r}^{2}$.由${S}_{四边形AD{O}_{1}E}=2{S}_{△AD{O}_{1}}=\sqrt{3}{r}^{2}$.
∵由题意,∠DO1E=120°,得${S}_{扇形{O}_{1}DE}=\frac{π}{3}{r}^{2}$,
∴圆形纸片不能接触到的部分的面积为3( $\sqrt{3}{r}^{2}-\frac{π}{3}{r}^{2}$)=(3$\sqrt{3}$-π)r2.
故答案为:$(3\sqrt{3}-π){r}^{2}$.
点评 本题考查了面积的计算、等边三角形的性质和切线的性质,是基础知识要熟练掌握.


科目:初中数学 来源: 题型:填空题
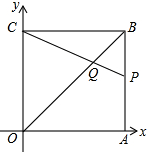 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
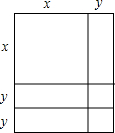 通过计算几何图形的面积可表示一些代数恒等式,小明从图中得到4个代数恒等式:①x(x+y)=x2+xy;②x2+3xy+2y2=(x+y)(x+2y);③(x+2y)2=x2+4xy+4y2;④x2+2xy+y2=(x+y)2.其中正确的有( )
通过计算几何图形的面积可表示一些代数恒等式,小明从图中得到4个代数恒等式:①x(x+y)=x2+xy;②x2+3xy+2y2=(x+y)(x+2y);③(x+2y)2=x2+4xy+4y2;④x2+2xy+y2=(x+y)2.其中正确的有( )| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
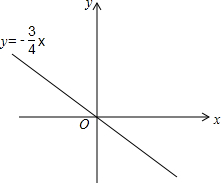 在平面直角坐标系xOy中,将直线y=-$\frac{3}{4}$x沿y轴向上平移6个单位后,分别与x轴、y轴相交于A,B两点.
在平面直角坐标系xOy中,将直线y=-$\frac{3}{4}$x沿y轴向上平移6个单位后,分别与x轴、y轴相交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com