
 著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空.
著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空. ∠AOB=75°,
∠AOB=75°, ∠BOC=30°,
∠BOC=30°, ∠AOB=70°,
∠AOB=70°, ∠AOB=60°,
∠AOB=60°, ∠BOC=25°,
∠BOC=25°, ∠AOC,
∠AOC, ∠BOC,∠AOM=∠MOB,要求∠MON,先求出∠MOC和∠NOC;
∠BOC,∠AOM=∠MOB,要求∠MON,先求出∠MOC和∠NOC;

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
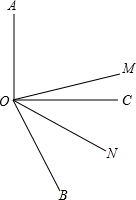 著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空.
著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com