
【题目】在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.

【答案】(1)证明见解析(2)当∠DAB等于35°时,四边形ADOE是菱形
【解析】试题分析:(1)根据直角三角形斜边中线等于斜边一半得:DN=![]() AB,由中位线定理得:OM=
AB,由中位线定理得:OM=![]() AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
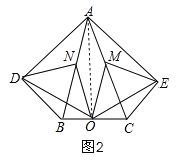
(2)连接AO,当∠DAB等于35°时,四边形ADOE是菱形,如图2,设∠DAB=x°,则∠BND=2x°,易证得OD=OE,AD=AE,因此只要AD=OD,四边形ADOE就是菱形;即∠DAO=∠AOD,列关于x的方程解出即可.
试题解析:证明:(1)∵∠ADB=90°,N是AB的中点,∴DN=![]() AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=
AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=![]() AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=
AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=![]() AB,OM=
AB,OM=![]() AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
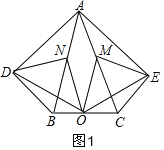
(2)当∠DAB等于35°时,四边形ADOE是菱形,理由是:
如图2,连接AO,设∠DAB=x°,则∠BND=2x°,∵AB=AC,O是BC的中点,∴AO平分∠BAC,AO⊥BC,∵∠BAC=40°,∴∠BAO=20°,在Rt△ABO中,N是AB的中点,∴ON=![]() AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=
AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=![]() AC,DN=
AC,DN=![]() AB,∴ON=DN,∴∠NDO=∠NOD=
AB,∴ON=DN,∴∠NDO=∠NOD=![]() (180°-∠DNO)=90°﹣
(180°-∠DNO)=90°﹣![]() (2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.
(2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在![]() 中,若
中,若![]() ,则
,则![]() 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.
(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
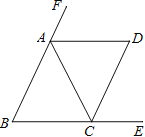
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() .
.
(1)![]() 满足何条件时,y随x的增大而减小;
满足何条件时,y随x的增大而减小;
(2)![]() 满足何条件时,图像经过第一、二、四象限;
满足何条件时,图像经过第一、二、四象限;
(3)![]() 满足何条件时,它的图像与y轴的交点在x轴的上方.
满足何条件时,它的图像与y轴的交点在x轴的上方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,点D在AC上,BC=BD,DE∥BC交AB于点E,则图中等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点0.
①求证:BE= AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N.求证:N是BD的中点.
注:第(2)问的解答过程无需注明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com