Question

当k为何值时，关于x的方程（k+2）x²-（2k+1）x+k=0．
（1）有两个实数根？
（2）对k选取一个合适的整数，使原方程有两个实数根，并求此时方程的根．

Answer 1

【答案】分析：（1）根据方程有两个相等的实数根可知△≥0，求出k的值即可；
（2）根据△＞0时方程有两个相等的实数根求出k的取值范围，在k的取值范围内找一个合适的整数，求出△的值，再利用求根公式求出方程的根即可．
解答：解：（1）∵于x的方程（k+2）x²-（2k+1）x+k=0．有两个实数根，
∴△=[-（2k+1）]²-4k（k+2）≥0，
∴k≤；

（2）∵由（1）可知k≤且k≠-2时方程有两个实数根，
∴设k=，此时△=0，
∴x===．
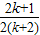
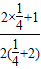
故答案为：k≤且k≠-2，．
点评：本题考查的是一元二次方程根的判别式，熟知一元二次方程根的情况与判别式△的关系是解答此题的关键．