
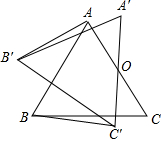
 已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.
已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.分析 (1)连接B'O,BO,根据旋转的性质以及等边三角形的性质,即可判定△AOB'≌△C'OB(SAS),进而得到AB′=BC′;
(2)连接BB',AC',根据A'B'∥BC,AB′=BC′,即可判定四边形AC′BB′是平行四边形,再根据AB=B'C',即可得到四边形AC′BB′是矩形.
解答 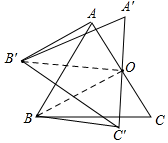 解:(1)如图,连接B'O,BO,
解:(1)如图,连接B'O,BO,
由旋转可得,B'O=BO,AO=A'O,C'O=CO,
∵O为AC边的中点,
∴AO=C'O,
∵△ABC、△A'B'C'都是等边三角形,
∴B'O⊥A'C',BO⊥AC,
∴∠AOB=∠C'OB',
∴∠AOB'=∠C'OB,
在△AOB'和△C'OB中,
$\left\{\begin{array}{l}{B'O=BO}\\{∠AOB'=∠C'OB}\\{AO=C'O}\end{array}\right.$,
∴△AOB'≌△C'OB(SAS),
∴AB′=BC′;
(2)四边形AC′BB′是矩形.
理由:如图,连接BB',AC',
当α=60°时,∠AOA'=60°=∠A',
∴∠OAA'=60°,
∵∠C=60°,
∴∠C=∠A'AO,
∴A'B'∥BC,
又∵AB′=BC′,
∴四边形AC′BB′是平行四边形,
又∵AB=B'C',
∴四边形AC′BB′是矩形.
点评 本题主要考查了旋转的性质,解题时注意:对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形全等.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
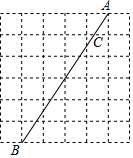 如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为点C,则AC:CB为( )
如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为点C,则AC:CB为( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=( )
如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=( )| A. | 2 | B. | 3 | C. | 4.5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
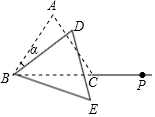 如图,等边三角形ABC中,AB=5,延长BC至点P,使CP=3,将△ABC绕点B顺时针旋转a角(0<a<60°),得到△DBE,连接DP、EP,则当△DPE为等腰三角形时,点D到直线BP的距离为3或$\frac{5}{2}$或$\frac{4\sqrt{3}-3}{5}$.
如图,等边三角形ABC中,AB=5,延长BC至点P,使CP=3,将△ABC绕点B顺时针旋转a角(0<a<60°),得到△DBE,连接DP、EP,则当△DPE为等腰三角形时,点D到直线BP的距离为3或$\frac{5}{2}$或$\frac{4\sqrt{3}-3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB'C'的位置,连接CC',若CC'∥AB,则旋转角α的度数为40°.
如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB'C'的位置,连接CC',若CC'∥AB,则旋转角α的度数为40°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
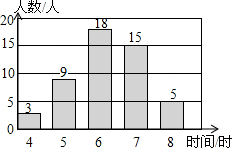 在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是120.
在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是120.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
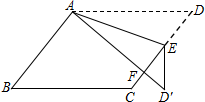 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com