
����Ŀ���������κ���y1=ax2+bx+c��һ�κ���y2=kx+m��ͼ��ʱ�����г��±���
x | �� | ��1 | 0 | 1 | 2 | 3 | 4 | 5 | �� |
y1 | �� | 0 | ��3 | ��4 | ��3 | 0 | 5 | 12 | �� |
y2 | �� | 0 | 2 | 4 | 6 | 8 | 10 | 12 | �� |
������ݱ�����Ϣ�ش��������⣬
��1�����κ���y1=ax2+bx+c��ͼ����y�ύ������Ϊ ��
��2����y1��y2ʱ���Ա���x��ȡֵ��Χ�� ��
��3����д�����κ���y1=ax2+bx+c��������ͬ�����ʣ�
���𰸡���1����0����3������2����x����1��x��5ʱ�����κ�����ֵ����һ�κ�����ֵ����3��������
��������
�����������1����x=0�����y����ֵ��ȷ����y�ύ�����꼴�ɣ�
��2�������ô���ϵ����������κ�����һ�κ����Ľ���ʽ�����������ͼ��Ľ��㣬�����ɵó����ۣ�
��3�����ö��κ��������ʣ����ڷ��Գ��ᣬ������ֱ�ӵó��𰸼��ɣ�
�⣺��1�����κ���y1=ax2+bx+c��ͼ����y�ύ������Ϊ��0����3����
��2��������ã�
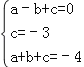 ��
��
���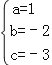 ��
��
�����κ����Ľ���ʽΪy=x2��2x��3=��x��1��2��4��
��һ�κ���y2=kx+m��ͼ����㣨��1��0������0��2����
��![]() ��
��
���![]() ��
��
��һ�κ����Ľ���ʽΪy=2x+2��
��ͼ��ʾ��
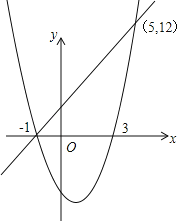
��x����1��x��5ʱ�����κ�����ֵ����һ�κ�����ֵ��
��3���ú�����ͼ�����ϣ���x=1ʱ�����������ֵ����x��1ʱ��y��x���������С����x��1ʱ��y��x�����������������Ϊ��1����4�����Գ���Ϊֱ��x=1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ֳ�������ܳ�Ϊ110m��Χ����ǽ��ǽ��Ϊ22m��Χ����ͼ��ʾ���������������AEHG�����CDEF��������ھ���BFHG�����һ�룬��AD��Ϊxm����������ABCD�����Ϊym2��
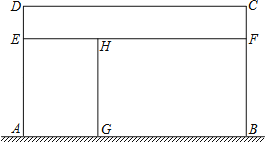
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����xΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
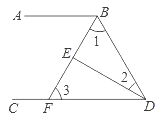
����Ŀ����ͼ����ABD�͡�BDC��ƽ���߽��ڵ�E��BE���ӳ��߽�CD�ڵ�F���ҡ�1+��2=90�㣮�����2���3�Ĺ�ϵ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij����1�������к�Сѧ���μ�ȫ���������������⣬Ϊ���˽�1����ѧ���ij��ɼ������г�ȡ500��ѧ�����ɼ�����ͳ�Ʒ��������������������500�ǣ� ��
A.����
B.����
C.һ������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x1 �� x2��һԪ���η���x2��2x��3=0����������x12+x22=�� ��
A.6
B.8
C.10
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������棺��¿��װ30��,ÿ���ۼ�300Ԫ.��һ���Թ�����10��ʱ,�ۼ۲��䣻��һ���Թ���10��ʱ��ÿ����1���������ÿ����װ���ۼ۾�����3Ԫ����֪�÷�װ�ɱ���ÿ��200Ԫ����˿�һ���Թ����װx��ʱ����������л���yԪ��
��1����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���˿�һ���Թ�����ټ�ʱ����������л�����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԫ���ڼ䣬ij�̼Ұ�ԭ��ΪaԪ��a��0�����·����20%��������20%�����̼����������·����ˣ��������ˣ����Dz��ⲻ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com