
【题目】已知,![]() ,
,![]() 分别在直线
分别在直线![]() 上,
上,![]() 是平面内一点,
是平面内一点,![]() 和
和![]() 的平分线所在直线相交于点
的平分线所在直线相交于点![]() .
.
(1)如图1,当![]() 都在直线
都在直线![]() 之间,且
之间,且![]() 时,
时,![]() 的度数为_________;
的度数为_________;
(2)如图2,当![]() 都在直线
都在直线![]() 上方时,探究
上方时,探究![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)如图3,当![]() 在直线
在直线![]() 两侧时,直接写出
两侧时,直接写出![]() 和
和![]() 之间的数量关系是_____.
之间的数量关系是_____.

【答案】(1)45°;(2)证明见解析;(3)![]() .
.
【解析】
(1)过E作EH∥AB,FG∥AB,根据平行线的性质得到∠BME=∠MEH,∠DNE=∠NEH,根据角平分线的定义得到∠BMF+∠DNF=![]() (∠BME+∠DNE)=45°,于是得到结论;(2)根据三角形的外角的性质得到∠E=∠EGB-∠EMB,根据平行线的性质得到∠EGB=∠END,∠FHB=∠FND,根据角平分线的定义得到∠EMB=2∠FMB,∠END=2∠FND,于是得到结论;(3)根据平行线的性质得到∠5=∠END,根据角平分线的定义得到∠5=∠END=2∠4,∠BME=2∠1=∠E+∠5=∠E+2∠4,根据三角形的外角的性质和四边形的内角和即可得到结论.
(∠BME+∠DNE)=45°,于是得到结论;(2)根据三角形的外角的性质得到∠E=∠EGB-∠EMB,根据平行线的性质得到∠EGB=∠END,∠FHB=∠FND,根据角平分线的定义得到∠EMB=2∠FMB,∠END=2∠FND,于是得到结论;(3)根据平行线的性质得到∠5=∠END,根据角平分线的定义得到∠5=∠END=2∠4,∠BME=2∠1=∠E+∠5=∠E+2∠4,根据三角形的外角的性质和四边形的内角和即可得到结论.
解:(1)过E作EH∥AB,过点F作FG∥AB,
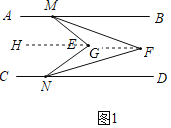
∵AB∥CD,
∴EH∥CD,FG∥CD,
∴∠BME=∠MEH,∠DNE=∠NEH,
∴∠BME+∠DNE=∠MEH+∠NEH=∠MEN=90°,
同理∠MFN=∠BMF+∠DNF,
∵MF平分∠BME,FN平分∠DNE,
∴∠BMF+∠DNF=![]() (∠BME+∠DNE)=45°,
(∠BME+∠DNE)=45°,
∴∠MFN的度数为45°;
故答案为:45°;
(2)∵∠EGB=∠EMB+∠E,
∴∠E=∠EGB-∠EMB,
∵AB∥CD,
∴∠EGB=∠END,∠FHB=∠FND,
∴∠E=∠END-∠EMB,
∵MF、NF分别平分∠BME和∠DNE,
∴∠EMB=2∠FMB,∠END=2∠FND,
∴∠E=2∠FND-2∠FMB=2(∠FND-∠FMB),
∵∠FHB=∠FMB+∠F,
∴∠F=∠FHB-∠FMB,
=∠FND-∠FMB,
∴∠E=2∠F;
(3)![]() ∠E+∠MFN=180°,
∠E+∠MFN=180°,
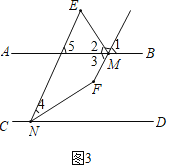
证明:∵AB∥CD,
∴∠5=∠END,
∵NF平分∠END,
∴∠5=∠END=2∠4,
∵MF平分∠BME,
∴∠BME=2∠1=∠E+∠5=∠E+2∠4,
∴∠3=∠1=![]() ∠E+∠4,
∠E+∠4,
∵∠E+∠MFN=360°-∠4-∠2-∠3=360°-∠4-(180°-∠E-2∠4)-(![]() ∠E+∠4)=180°+
∠E+∠4)=180°+![]() ∠
∠
∴∠MFN+![]() ∠E=180°.
∠E=180°.
故答案为:![]() ∠E+∠MFN=180°.
∠E+∠MFN=180°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角![]() 中,
中,![]() 是
是![]() 边上的高.
边上的高. ![]() ,且
,且![]()
![]() .连接
.连接![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定正确的个数是( )
.其中一定正确的个数是( )

A.![]() 个B.
个B.![]() 个
个
C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生整体的数学学习能力,年级组织了“数学钻石活动”,从中随机抽取部分学生的成绩进行统计分析,整理得到如下不完整的频数分布表和数分布直方图:


(1)表中的![]() ,
,![]() ;
;
(2)把上面的频数分布直方图补充完整;
(3)根据调查结果,估计年级500名学生中,成绩不低于85分的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于第一、三象限内的
的图像交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,且四边形
,且四边形![]() 是平行四边形,点
是平行四边形,点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求该反比例函数和一次函数的表达式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
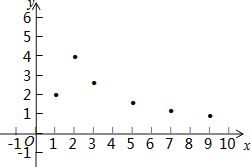
【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:

小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为_____________;
②该函数的一条性质:_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,
的小数部分我们不可能全部写出来,![]() ,于是可用
,于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是________,小数部分是________.
的整数部分是________,小数部分是________.
(2)如果![]() 的小数部分为
的小数部分为![]() ,
,![]() 的整数部分为
的整数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的相反数.
的相反数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com