
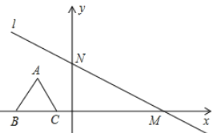
【题目】如图,在平面直角坐标系中,有一条直线l:y=![]() +4与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移
+4与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移
(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标;
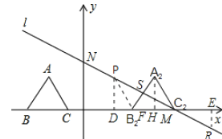
(2)继续向右平移,得到△A2B2C2,此时△A2B2C2的三边中垂线的交点P(即外心)恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
【答案】(1)A1点的坐标是(![]() ,3),(2)P(3
,3),(2)P(3![]() ,1);(3)存在四个点,分别是P(3
,1);(3)存在四个点,分别是P(3![]() ,1),Q(
,1),Q(![]() ,3),S(4
,3),S(4![]() 3,
3,![]() ),R.(4
),R.(4![]() +3,
+3,![]() ).
).
【解析】
(1)根据等边三角形ABC的高为3,得出A1点的纵坐标为3,再代入y=![]() +4即可;
+4即可;
(2)设P(x,y),连接A2P并延长交x轴于点H,连接B2P,先求出A2B2=2![]() ,HB2=
,HB2=![]() ,根据点P是等边三角形A2B2C2的外心,得出PH=1,将y=1代入y=
,根据点P是等边三角形A2B2C2的外心,得出PH=1,将y=1代入y=![]() +4,即可得出点P的坐标;
+4,即可得出点P的坐标;
(3)根据点P是等边三角形A2B2C2的外心,得出△PA2B2,△PB2C2,△PA2C2是等腰三角形,得P(3![]() ,1),由(2)得,C2(4
,1),由(2)得,C2(4![]() ,0),点C2满足直线y=
,0),点C2满足直线y=![]() +4的关系式,得出点C2与点M重合,∠PMB2=30°,设点Q满足的条件,△QA2B2,△B2QC2,△A2QC2能构成等腰三角形,则QA2=QB2,B2Q=B2C2,A2Q=A2C2,作QD⊥x轴与点D,连接QB2,根据QB2=2
+4的关系式,得出点C2与点M重合,∠PMB2=30°,设点Q满足的条件,△QA2B2,△B2QC2,△A2QC2能构成等腰三角形,则QA2=QB2,B2Q=B2C2,A2Q=A2C2,作QD⊥x轴与点D,连接QB2,根据QB2=2![]() ,∠QB2D=2∠
,∠QB2D=2∠![]() ,3),设点S满足的条件,△SA2B2,△C2B2S,△C2SA2是等腰三角形,则SA2=SB2,C2B2=C2S,C2A2=C2S,作SF⊥x轴于点F,根据SC2=2
,3),设点S满足的条件,△SA2B2,△C2B2S,△C2SA2是等腰三角形,则SA2=SB2,C2B2=C2S,C2A2=C2S,作SF⊥x轴于点F,根据SC2=2![]() ,∠SB2C2=∠PMB2=30°,求出S(4
,∠SB2C2=∠PMB2=30°,求出S(4![]() 3,
3,![]() ),设点R满足的条件,△RA2B2,△C2B2R,△C2A2R能构成等腰三角形,则RA2=RB2,C2B2=C2R,C2A2=C2R,作RE⊥x轴于点E,根据RC2=2
),设点R满足的条件,△RA2B2,△C2B2R,△C2A2R能构成等腰三角形,则RA2=RB2,C2B2=C2R,C2A2=C2R,作RE⊥x轴于点E,根据RC2=2![]() ,∠RC2E=∠PMB2=30°,R(4
,∠RC2E=∠PMB2=30°,R(4![]() +3,
+3,![]() ).
).
(1)∵等边三角形ABC的高为3,
∴A1点的纵坐标为3,
∵顶点A1恰落在直线l上,
∴3=![]() +4,
+4,
解得;x=![]() ,
,
∴A1点的坐标是(![]() ,3),
,3),
故答案为:(![]() ,3);
,3);
(2)设P(x,y),连接A2P并延长交x轴于点H,连接B2P,
在等边三角△A2B2C2中,高A2H=3,
∴A2B2=2![]() ,HB2=
,HB2=![]() ,
,
∵点P是等边三角形A2B2C2的外心,
∴∠PB2H=30°,
∴PH=1,即y=1,
将y=1代入y=![]() +4,
+4,
解得:x=3![]() .
.
∴P(3![]() ,1);
,1);
(3)∵点P是等边三角形A2B2C2的外心,
∴△PA2B2,△PB2C2,△PA2C2是等腰三角形
∴点P满足的条件,由(2)得P(3![]() ,1),
,1),
由(2)得,C2(4![]() ,0),点C2满足直线y=
,0),点C2满足直线y=![]() +4的关系式,
+4的关系式,
∴点C2与点M重合
∴∠PMB2=30°,
设点Q满足的条件,△QA2B2,△B2QC2,△A2QC2能构成等腰三角形,
此时QA2=QB2,B2Q=B2C2,A2Q=A2C2,
作QD⊥x轴与点D,连接QB2,
∵QB2=2![]() ,∠QB2D=2∠PMB2=60°,
,∠QB2D=2∠PMB2=60°,
∴QD=3,
∴Q(![]() ,3),
,3),
设点S满足的条件,△SA2B2,△C2B2S,△C2SA2是等腰三角形,
此时SA2=SB2,C2B2=C2S,C2A2=C2S,
作SF⊥x轴于点F,
∵SC2=2![]() ,∠SB2C2=∠PMB2=30°,
,∠SB2C2=∠PMB2=30°,
∴SF=![]() ,
,
∴S(4![]() 3,
3,![]() ),
),
设点R满足的条件,△RA2B2,△C2B2R,△C2A2R能构成等腰三角形,
此时RA2=RB2,C2B2=C2R,C2A2=C2R,
作RE⊥x轴于点E,
∵RC2=2![]() ,∠RC2E=∠PMB2=30°,
,∠RC2E=∠PMB2=30°,![]() ,
,
∴R(4![]() +3,
+3,![]() ).
).
答:存在四个点,分别是P(3![]() ,1),Q(
,1),Q(![]() ,3),S(4
,3),S(4![]() 3,
3,![]() ),R.(4
),R.(4![]() +3,
+3,![]() ).
).


科目:初中数学 来源: 题型:
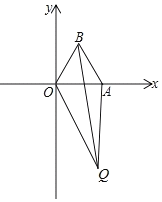
【题目】在平面直角坐标系中,O(0,0)、B(a,b),且a、b满足1﹣2a+a2+(b![]() )2=0.
)2=0.
(1)求a,b的值;
(2)若点A在x轴正半轴上,且OA=2,在平面内有一动点Q(不在x轴上),QO=m,QA=n,QB=p,且p2=m2+n2,求∠OQA的度数.
(3)阅读以下内容:对于实数a、b有(a﹣b)2≥0,∴a2﹣2ab+b2≥0,
即a2+b2≥2ab.
利用以上知识,在(2)的条件下求△AOQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过小学的学习我们知道,分数可分为“真分数”和“假分数”,并且假分数都可化为带分数.类比分数,对于分式也可以定义:对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:![]()
解决下列问题:
(1)分式![]() 是________分式(填“真”或“假”);
是________分式(填“真”或“假”);
(2)假分式![]() 可化为带分式_________的形式;请写出你的推导过程;
可化为带分式_________的形式;请写出你的推导过程;
(3)如果分式![]() 的值为整数,那么
的值为整数,那么![]() 的整数值为_________.
的整数值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(4,6),直线y=kx+3k将平行四边形OABC分割成面积相等的两部分,则k的值是( ).

A.![]() B.
B.![]() C.-
C.-![]() D.﹣
D.﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P)在![]() 轴上行驶.试确定下列情况下汽车(点P)的位置:
轴上行驶.试确定下列情况下汽车(点P)的位置:
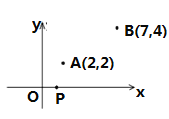
(1)求直线AB的解析式,且确定汽车行驶到什么点时到A、B两村距离之差最大?
(2)汽车行驶到什么点时,到A、B两村距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千 克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)(3分)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)(3分)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)(4分)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=![]() x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
(1)求抛物线的解析式;
(2)若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元
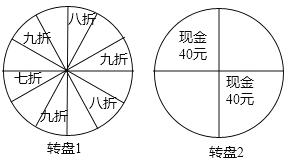
(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com