
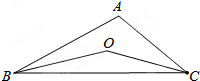
 如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°.
如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°. 分析 根据三角形的角平分线定义和三角形的内角和定理求出∠OBC+∠OCB的度数,再根据三角形的内角和定理即可求出∠BOC的度数.
解答 解:∵OB、OC分别是∠ABC和∠ACB的角平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB),
∵∠A=100°,
∴∠OBC+∠OCB=$\frac{1}{2}$(180°-100°)=40°,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-40°
=140°.
故答案为:140°
点评 本题主要利用角平分线的定义和三角形内角和定理求解,熟记概念和定理是解题的关键.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 方差 | C. | 中位数 | D. | 平均数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图中矩形ABCD的四个顶点位于双曲线y=$\frac{1}{x}$上,且SABCD=2$\sqrt{5}$,则xA=( )
如图中矩形ABCD的四个顶点位于双曲线y=$\frac{1}{x}$上,且SABCD=2$\sqrt{5}$,则xA=( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\frac{3-\sqrt{5}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com