某篮球队12名队员的年龄如表：
| 年龄（岁） | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和平均数分别是（ ）
|
| A． | 18，19 | B． | 19，19 | C． | 18，19.5 | D． | 19，19.5 |
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目：初中数学 来源： 题型：
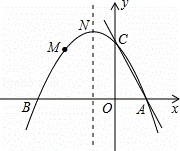
如图，抛物线y=ax2+bx+c（a≠0）的图象过点M（﹣2，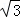
），顶点坐标为N（﹣1，
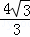），且与x轴交于A、B两点，与y轴交于C点．
（1）求抛物线的解析式；
（2）点P为抛物线对称轴上的动点，当△PBC为等腰三角形时，求点P的坐标；
（3）在直线AC上是否存在一点Q，使△QBM的周长最小？若存在，求出Q点坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，在平面直角坐标系中，二次函数y=﹣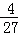
x2+12的图象与y轴交于点A，与x轴交于B，C两点（点B在点C的左侧），连接AB，AC．
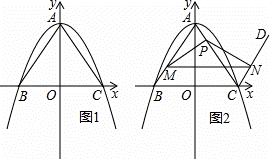
（1）点B的坐标为 ，点C的坐标为 ；
（2）过点C作射线CD∥AB，点M是线段AB上的动点，点P是线段AC上的动点，且始终满足BM=AP（点M不与点A，点B重合），过点M作MN∥BC分别交AC于点Q，交射线CD于点N （点 Q不与点P重合），连接PM，PN，设线段AP的长为n．
①如图2，当n＜
AC时，求证：△PAM≌△NCP；
②直接用含n的代数式表示线段PQ的长；
③若PM的长为
，当二次函数y=﹣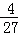x2+12的图象经过平移同时过点P和点N时，请直接写出此时的二次函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
某小区为了排污，需铺设一段全长为720米的排污管道，为减少施工对居民生活的影响，须缩短施工时间，实际施工时每天的工作效率比原计划提高20%，结果提前2天完成任务．设原计划每天铺设x米，下面所列方程正确的是（ ）
|
| A． |
| B． |
|
|
| C． |
| D． |
|
查看答案和解析>>
科目：初中数学 来源： 题型：
数学问题：计算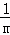
+
+
+…+
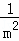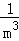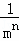（其中m，n都是正整数，且m≥2，n≥1）．
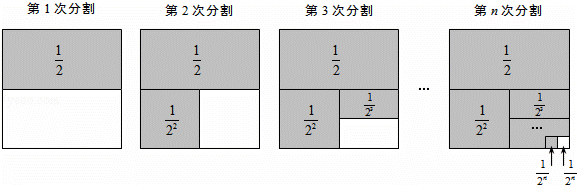
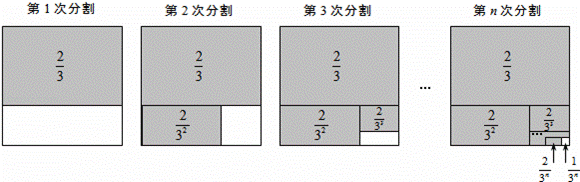
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算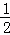
+
+
+…+
．
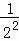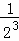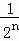第1次分割，把正方形的面积二等分，其中阴影部分的面积为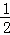
；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为+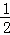
；
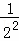第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为++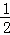
+…+
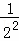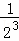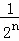，最后空白部分的面积是．
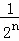根据第n次分割图可得等式：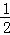
+
+
+…+
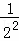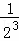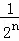=1﹣．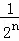
探究二：计算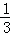
+
+
+…+
．
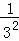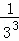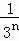第1次分割，把正方形的面积三等分，其中阴影部分的面积为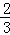
；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为+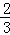
；
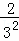第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为++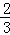
+…+
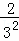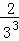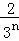，最后空白部分的面积是
．
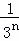根据第n次分割图可得等式：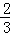
+
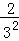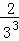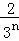++…+=1﹣，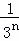
两边同除以2，得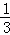
+
+
+…+
=
﹣
．
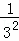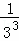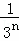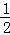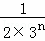探究三：计算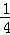
+
+
+…+
．
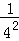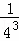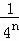（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算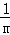
+
+
+…+
．
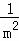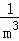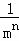（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式：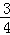 
+
+
+…+
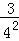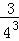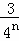=1﹣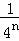
，
所以，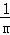
+
+
+…+
= 
﹣
．
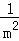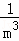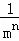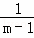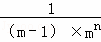拓广应用：计算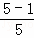 
+
+
+…+
．
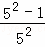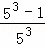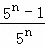查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，自变量x的取值范围是 ．
﹣
=2
﹣
=