
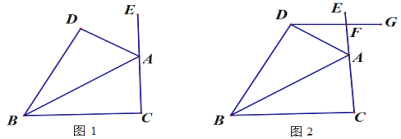
【题目】已知:如图,AB平分∠CBD,∠DBC=60°,∠C=∠D.
(1)若AC⊥BC,求∠BAE的度数;
(2)请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图,过点D作DG∥BC交CE于点F,当∠EFG=2∠DAE时,求∠BAD的度数.
【答案】(1)∠BAE==120°;(2)结论:∠DAE=2∠C—120°.证明见解析;(3)∠BAD=66°.
【解析】
(1)根据角平分线的性质得到∠CBD=60°,由于∠BAE是△ABC的外角,则可以得到答案.
(2)根据三角形内角和性质和四边形内角和,进行计算即可得到答案.
(3)根据对顶角的性质可得∠EFG=∠DFA,根据平行线的性质得2∠DAE +∠C=180°,
再根据角平分线的性质即可得到答案.
解:∵AC⊥BC
∴∠BCA=90°,
∵AB平分∠CBD,
∴∠ABC=![]() ∠CBD, ∠CBD=60°,
∠CBD, ∠CBD=60°,
∴∠ABC=30°,
∵∠BAE是△ABC的外角,
∴∠BAE=∠BCA+∠ABC=120°.
结论:∠DAE=2∠C—120°.
证明:∵∠DAE+∠DAC=180°,
∴∠DAC =180°—∠DAE,
∵∠DAC+∠DBC+∠C +∠D =360°,
∴180—∠DAE+∠DBC+∠C +∠D =360°,
∵∠DBC=60°,∠C=∠D,
∴2∠C—∠DAE=120°,
∴∠DAE=2∠C—120°.
解:∵∠EFG和∠DFA是对顶角,
∴∠EFG=∠DFA,
∵∠EFG=2∠DAE,
∴∠DFA=2∠DAE,
∵DG∥BC,
∴∠DFA+∠C=180°,
∴2∠DAE +∠C=180°,
∵∠DAE=2∠C—120°,
∴∠DAE=48°,
∴∠DAC =132°,
∵AB平分∠CBD,
∴∠DBA=∠CBA,
∵∠C=∠D,
∴∠BAD=∠BAC,
∴∠BAD=![]() ∠DAC=66°
∠DAC=66°


科目:初中数学 来源: 题型:
【题目】(1)已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
(2)分解因式:
①x2-8xy+16y2
②(x+y+1)2-(x-y+1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为D.
的顶点为D.
(1)求点D的坐标(用含m的代数式表示);
(2)若该抛物线经过点A(1,m),求m的值;
(3)在(2)的条件下,抛物线与x轴是否有交点,若有,求出交点坐标,若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A ,D,B,E在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF 的是( )

A.BC = EFB.AC//DFC.∠C = ∠FD.∠BAC = ∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() 为边
为边![]() 的中点.
的中点. ![]() 是
是![]() 上一点,⊙
上一点,⊙![]() 与
与![]() 相切于点
相切于点![]() ,且与
,且与![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() .连接
.连接![]() 交
交![]() 于点
于点![]() .
.

(![]() )求证:
)求证: ![]() .
.
(![]() )已知
)已知![]() ,
, ![]() .当
.当![]() 是⊙
是⊙![]() 的直径时,求
的直径时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
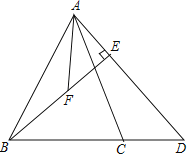
【题目】如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=![]() ,AE=
,AE=![]() ,求BE的长;
,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com