
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŅ»Õų¤·½ŠĪÖ½ĢõÉĻ»Ņ»ĢõŹżÖį£®
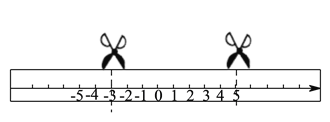
£Ø![]() £©ČōÕŪµžÖ½Ģõ£¬ŹżÖįÉĻ±ķŹ¾
£©ČōÕŪµžÖ½Ģõ£¬ŹżÖįÉĻ±ķŹ¾![]() µÄµćÓė±ķŹ¾
µÄµćÓė±ķŹ¾![]() µÄµćÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£®
µÄµćÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£®
£Ø![]() £©Čō¾¹żÄ³“ĪÕŪµžŗó£¬øĆŹżÖįÉĖµÄĮ½øöŹż
£©Čō¾¹żÄ³“ĪÕŪµžŗó£¬øĆŹżÖįÉĖµÄĮ½øöŹż![]() ŗĶ
ŗĶ![]() ±ķŹ¾µÄµćĒ”ŗĆÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£ØÓĆŗ¬
±ķŹ¾µÄµćĒ”ŗĆÖŲŗĻ£¬ŌņÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹżĪŖ__________£ØÓĆŗ¬![]() £¬
£¬ ![]() µÄ“śŹżŹ½±ķŹ¾£©£®
µÄ“śŹżŹ½±ķŹ¾£©£®
£Ø![]() £©Čō½«“ĖÖ½ĢõŃŲŠéĻß“¦¼ōæŖ£¬½«ÖŠ¼äµÄŅ»¶ĪÖ½Ģõ¶ŌÕŪ£¬Ź¹Ęä×óÓŅĮ½¶ĖÖŲŗĻ£¬ÕāŃłĮ¬Šų¶ŌÕŪ
£©Čō½«“ĖÖ½ĢõŃŲŠéĻß“¦¼ōæŖ£¬½«ÖŠ¼äµÄŅ»¶ĪÖ½Ģõ¶ŌÕŪ£¬Ź¹Ęä×óÓŅĮ½¶ĖÖŲŗĻ£¬ÕāŃłĮ¬Šų¶ŌÕŪ![]() “Īŗó£¬ŌŁ½«ĘäÕ¹æŖ£¬Ēė·Ö±šĒó³ö×ī×ó¶ĖµÄÕŪŗŪŗĶ×īÓŅ¶ĖµÄÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹż£ØÓĆŗ¬
“Īŗó£¬ŌŁ½«ĘäÕ¹æŖ£¬Ēė·Ö±šĒó³ö×ī×ó¶ĖµÄÕŪŗŪŗĶ×īÓŅ¶ĖµÄÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹż£ØÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾£©£®
µÄ“śŹżŹ½±ķŹ¾£©£®
”¾“š°ø”æ(1)-1;(2) ![]() ;(3)
;(3) ![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÕŅ³ö5±ķŹ¾µÄµćÓė-3±ķŹ¾µÄµć×é³ÉĻ߶ĪµÄÖŠµć±ķŹ¾Źż£¬Č»ŗó½įŗĻŹżÖį¼“æÉĒóµĆ“š°ø£»
£Ø2£©ĻČÕŅ³öa±ķŹ¾µÄµćÓėb±ķŹ¾µÄµćĖł×é³ÉĻ߶ĪµÄÖŠµć£¬“Ó¶ųæÉĒóµĆ“š°ø£»
£Ø3£©ĻČĒó³öĆæĮ½ĢõĻąĮŚÕŪŗŪµÄ¾ąĄė£¬½ųŅ»²½µĆµ½×ī×ó¶ĖµÄÕŪŗŪŗĶ×īÓŅ¶ĖµÄÕŪŗŪÓėŹżÖįµÄ½»µć±ķŹ¾µÄŹż£¬¼“æÉĒóµĆ“š°ø£®
ŹŌĢā½āĪö£ŗ£Ø![]() £©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ
£©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ![]() ŗĶ
ŗĶ![]() µÄÖŠµć
µÄÖŠµć![]() £®
£®
£Ø![]() £©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ
£©ÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ![]() ŗĶ
ŗĶ![]() µÄÖŠµć
µÄÖŠµć![]() £®
£®
£Ø![]() £©×ī×ó¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ
£©×ī×ó¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ ![]() £®×īÓŅ¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ
£®×īÓŅ¶ĖÕŪŗŪÓėŹżÖį½»µć±ķŹ¾µÄŹżĪŖ£ŗ ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠÓļ¾äÖŠ£¬“ķĪóµÄŹĒ£Ø £©
A.Ņ»ĢõÖ±ĻßÓŠĒŅÖ»ÓŠŅ»Ģõ“¹Ļß
B.²»ĻąµČµÄĮ½øö½ĒŅ»¶Ø²»ŹĒ¶Ō¶„½Ē
C.Ö±½ĒµÄ²¹½Ē±ŲŹĒÖ±½Ē
D.Į½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅņŹ½·Ö½āx2+mx©12£½£Øx+p£©£Øx+q£©£¬ĘäÖŠm”¢p”¢q¶¼ĪŖÕūŹż£¬ŌņÕāŃłµÄmµÄ×ī“óÖµŹĒ£Ø””””£©
A. 1 B. 4 C. 11 D. 12
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĶ¼ŹĒÓÉŅ»Š©»š²ń°ō“ī³ÉµÄĶ¼°ø£ŗ

£Ø1£©°ŚµŚ¢ŁøöĶ¼°øÓĆ øł»š²ń°ō£¬°ŚµŚ¢ŚøöĶ¼°øÓĆ øł»š²ń°ō£¬°ŚµŚ¢ŪøöĶ¼°øÓĆ øł»š²ń°ō£®
£Ø2£©°“ÕÕÕāÖÖ·½Ź½°ŚĻĀČ„£¬°ŚµŚnøöĶ¼°øÓƶąÉŁøł»š²ń°ō£æ
£Ø3£©¼ĘĖćŅ»ĻĀ°Ś121øł»š²ń°ōŹ±£¬ŹĒµŚ¼øøöĶ¼°ø£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬ACŹĒĻŅ£¬”ĻBACµÄĘ½·ÖĻß½»”ŃOÓŚµćD£¬¹żµćD×÷DE”ĶAC½»ACµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓBD”£

£Ø1£©ĒóÖ¤£ŗDEŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čōtan”ĻABD=2£¬CE=1£¬Ēó”ŃOµÄ°ė¾¶”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠµÄČĪŅāĮ½µćP£Øx1£¬y1£©£¬Q£Øx2£¬y2£©£¬ĪŅĆĒ°Ń|x1-x2|+|y1-y2|½ŠP£¬QĮ½µć¼äµÄ”°Ę½Ćę¾ąĄė”±£¬¼Ē×÷d£ØP£¬Q£©”£
£Ø1£©ŅŃÖŖOĪŖ×ų±źŌµć£¬¶ÆµćM£Øx£¬y£©ŹĒ×ų±źÖįÉĻµÄµć£¬Āś×ćd£ØO£¬M£©=l£¬ĒėŠ“³öµćMµÄ×ų±ź”£“š£ŗ ________£»
£Ø2£©ÉčP0£Øx0£¬y0£©ŹĒĘ½ĆęÉĻŅ»µć£¬Q0£Øx£¬y£©ŹĒÖ±Ļßl£ŗy=kx+bÉĻµÄ¶Æµć£¬ĪŅĆĒ¶ØŅåd£ØP0£¬Q0£©µÄ×īŠ”Öµ½Š×öP0µ½Ö±ĻßlµÄ”°Ę½Ćę¾ąĄė”±”£ŹŌĒóµćM£Ø2£¬1£©µ½Ö±Ļßy=x+2µÄ”°Ę½Ćę¾ąĄė”±”£
£Ø3£©ŌŚÉĻĆęµÄ¶ØŅå»ł“”ÉĻ£¬ĪŅĆĒæÉŅŌ¶ØŅåĘ½ĆęÉĻŅ»ĢõÖ±ĻßlÓė”ŃCµÄ”°Ö±½Ē¾ąĄė”±£ŗŌŚÖ±ĻßlÓė”ŃCÉĻø÷×ŌČĪČ”Ņ»µć£¬“ĖĮ½µćÖ®¼äµÄ”°Ę½Ćę¾ąĄė”±µÄ×īŠ”Öµ³ĘĪŖÖ±ĻßlÓė”ŃOµÄ”°Ę½Ćę¾ąĄė”±£¬¼Ē×÷d£Øl£¬”ŃC£©”£
ŹŌĒóÖ±Ļßy=x+2ÓėŌ²ŠÄŌŚÖ±½Ē×ų±źĻµŌµć”¢°ė¾¶ŹĒ1µÄ”ŃOµÄÖ±½Ē¾ąĄėd£Øl£¬”ŃO£©=__________”££ØÖ±½ÓŠ“³ö“š°ø£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄ·½³Ģx2-6mx+9m2-9=0”£
£Ø1£©ĒóÖ¤£ŗ“Ė·½³ĢÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£»
£Ø2£©Éč“Ė·½³ĢµÄĮ½øöøł·Ö±šĪŖx1”¢x2”£Čō2x1=x2-3£¬ĒómµÄÖµ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij°ą”°ŹżŃ§ŠĖȤŠ”×é”±¶ŌŗÆŹży=x2©2|x|µÄĶ¼ĻóŗĶŠŌÖŹ½ųŠŠĮĖĢ½¾æ£¬Ģ½¾æ¹ż³ĢČēĻĀ£¬Ēė²¹³äĶźÕū£®£Ø1£©×Ō±äĮæxµÄȔֵ·¶Ī§ŹĒČ«ĢåŹµŹż£¬xÓėyµÄ¼ø×é¶ŌÓ¦ÖµĮŠ±ķČēĻĀ£ŗ
x | ” | ©3 | © | ©2 | ©1 | 0 | 1 | 2 |
| 3 | ” |
y | ” | 3 |
| m | ©1 | 0 | ©1 | 0 |
| 3 | ” |
ĘäÖŠ£¬m=””””£®
£Ø2£©øł¾Ż±ķÖŠŹż¾Ż£¬ŌŚČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠĆčµć£¬²¢»³öĮĖŗÆŹżĶ¼ĻóµÄŅ»²æ·Ö£¬Ēė»³öøĆŗÆŹżĶ¼ĻóµÄĮķŅ»²æ·Ö£®
£Ø3£©¹Ū²ģŗÆŹżĶ¼Ļ󣬊“³öĮ½ĢõŗÆŹżµÄŠŌÖŹ£®
£Ø4£©½ųŅ»²½Ģ½¾æŗÆŹżĶ¼Ļó·¢ĻÖ£ŗ
¢ŁŗÆŹżĶ¼ĻóÓėxÖįÓŠ””””øö½»µć£¬ĖłŅŌ¶ŌÓ¦µÄ·½³Ģx2©2|x|=0ÓŠ”” ””øöŹµŹżøł£»
¢Ś·½³Ģx2©2|x|=2ÓŠ””””øöŹµŹżøł.

¢Ū¹ŲÓŚxµÄ·½³Ģx2©2|x|=aÓŠ4øöŹµŹżøłŹ±£¬aµÄȔֵ·¶Ī§ŹĒ”” £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°“ĻĀĮŠ³ĢŠņ¼ĘĖć£¬°Ń“š°øĢīŠ“ŌŚ±ķøńĄļ£¬Č»ŗóæ“æ“ÓŠŹ²Ć“¹ęĀÉ£¬ĻėĻėĪŖŹ²Ć“»įÓŠ
Õāøö¹ęĀÉ£æ
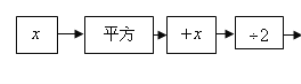

£Ø1£©ĢīŠ“±ķÄŚæÕøń£ŗ
ŹäČė | 3 | 2 | £2 |
| ” |
Źä³ö“š°ø | 0 | ” |
£Ø2£©Äć·¢ĻֵĹęĀÉŹĒ____________.
£Ø3£©ÓĆ¼ņŅŖ¹ż³ĢĖµĆ÷Äć·¢ĻֵĹęĀɵÄÕżČ·ŠŌ.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com