
【题目】基本模型:如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE~△BCF. 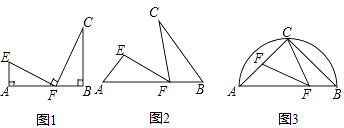
(1)模型拓展:如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE~△BCF;
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4 ![]() ,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】为体现社会对教师的尊重,教师节这天上午,出租车司机小王在东西走向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下.(单位:千米)+15,﹣4,+13,﹣10,﹣12,+3,﹣13,﹣17
(1)当最后一名老师到达目的地时,小王距离开始接送第一位老师之前的地点的距离是多少?
(2)若出租车的耗油量为0.4升/千米,这天上午出租车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+3|+|b-2|=0,A,B 之间的距离记为|AB|.请回答问题:
(1)直接写出a,b, |AB|的值. a= ,b = , |AB|= ;
(2)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(3)若点P在点A的左侧,M、N分别是PA、PB的中点.当点P在点A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距20km,B在A的北偏东45°方向上,一森林保护中心P在A的北偏东30°和B的正西方向上,现计划修建的一条高速公路将经过AB(线段),已知森林保护区的范围在以点P为圆心,半径为4km的圆形区域内,请问这条高速公路会不会穿越保护区?为什么?(sin15°=0.259,cos15°=0.966,tan15°=0.268) 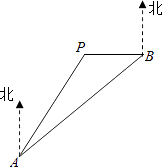
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有( ) 
A.L,K
B.C
C.K
D.L,K,C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P与y轴相切,交直线y=x于A,B两点,已知圆心P的坐标为(2,a)(a>2),AB=2 ![]() ,则a的值为( )
,则a的值为( ) 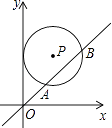
A.4
B.2+ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当![]() 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当![]() 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l:![]() 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线![]() 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com