
 的值(用含α的三角函数表示).
的值(用含α的三角函数表示).
 =
= =tanα,由此可知:当α=45°时,MM′=NN′;当α≠45°时,MM′≠NN′.
=tanα,由此可知:当α=45°时,MM′=NN′;当α≠45°时,MM′≠NN′. .
. (或
(或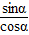 ). (10分)
). (10分) (或
(或 ). (12分)
). (12分)
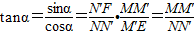 ,
, (或
(或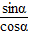 ). (10分)
). (10分)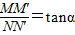 (或
(或 ). (12分)
). (12分)

科目:初中数学 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(党湾镇中 王建兴)(解析版) 题型:解答题
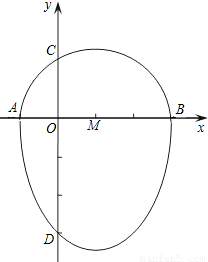 (2008•益阳)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
(2008•益阳)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《锐角三角函数》(06)(解析版) 题型:解答题
 的值(用含α的三角函数表示).
的值(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《图形的相似》(07)(解析版) 题型:解答题
 的值(用含α的三角函数表示).
的值(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《三角形》(20)(解析版) 题型:解答题
 的值(用含α的三角函数表示).
的值(用含α的三角函数表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com