
如图,平面直角坐标系中,矩形OABC的对角线AC=12,tan∠ACO= ,
,
(1)求B、C两点的坐标;
(2)把矩形沿直线DE对折使点C落在点A处,DE与AC相交于点F,求直线DE的解析式;
(3)若点M在直线DE上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)C的坐标是:(6 ,0),B的坐标是(6
,0),B的坐标是(6 ,6)。
,6)。
(2)直线DE的解析式是:y= x﹣6。
x﹣6。
(3)N的坐标是:(3, )或(﹣3,
)或(﹣3, )或(
)或( ,3)。
,3)。
解析试题分析:(1)根据三角函数求得OA以及OC的长度,则C、B的坐标即可得到。
解:在直角△OAC中, ,
,
∴设OA= x,则OC=3x,
x,则OC=3x,
根据勾股定理得:(3x)2+( x)2=AC2,即9x2+3x2=144,解得:x=2
x)2=AC2,即9x2+3x2=144,解得:x=2 。
。
∴C的坐标是:(6 ,0),B的坐标是(6
,0),B的坐标是(6 ,6)。
,6)。
(2)直线DE是AC的中垂线,应用待定系数法以及锐角三角函数定义即可求得DE的解析式。
解:∵F是AC的中点,∴根据对折的性质,F的坐标是(3 ,3)。
,3)。
设D(d,0),则根据对折的性质,E( ,6)。
,6)。
如图,过点E作EH⊥OC于点H,则HE=6,DH= 。
。
易证∠DEH=∠ACO,
∵ ,∴
,∴ ,
,
即 ,解得
,解得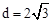 。
。
∴D( ,0)
,0)
设直线DE的解析式是y=" k" x+b,将点D、F的坐标代入,得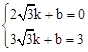 ,解得
,解得
∴直线DE的解析式是:y= x﹣6。
x﹣6。
(3)分当FM是菱形的边和当OF是对角线两种情况进行讨论,利用三角函数即可求得N的坐标:
OF= AC=6。
AC=6。
∵ ,
,
∴ 30°。∴DE与x轴夹角是60°。
30°。∴DE与x轴夹角是60°。
当FM是菱形的边时(如图),ON∥FM,
则∠NOC=60°或120°。
当∠NOC=60°时,过N作NG⊥y轴,
∴NG=ON•sin30°=6× =3,OG=ON•cos30°=6×
=3,OG=ON•cos30°=6× =
= 。
。
∴N的坐标是(3, )。
)。
当∠NOC=120°时,与当∠NOC=60°时关于原点对称,则N的坐标是(﹣3, )。
)。
当OF是对角线时(如图),MN关于OF对称。
∵F的坐标是( ,3),∴∠FOD=∠NOF=30°。
,3),∴∠FOD=∠NOF=30°。
在Rt△ONH中,OH= OF=3,
OF=3, 。
。
作NL⊥y轴于点L,
在Rt△ONL中,∠NOL=30°,
∴NL= ON=
ON= ,OL=ON•cos30°=2
,OL=ON•cos30°=2 ×
× =3。
=3。
∴N的坐标是( ,3)。
,3)。
综上所述,N的坐标是:(3, )或(﹣3,
)或(﹣3, )或(
)或( ,3)。
,3)。


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题:
(1)求整齐摆放在桌面上饭碗的高度y(cm)与饭碗数x(个)之间的一次函数解析式;
(2)把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.
(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某游泳池有水4000m3,先放水清洗池子.同时,工作人员记录放水的时间x(单位:分钟)与池内水量y(单位:m3) 的对应变化的情况,如下表:
| 时间x(分钟) | … | 10 | 20 | 30 | 40 | … |
| 水量y(m3) | … | 3750 | 3500 | 3250 | 3000 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,什么情况下到甲商场购买更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC﹣CD﹣DE,如图所示,从甲队开始工作时计时.
(1)分别求线段BC、DE所在直线对应的函数关系式.
(2)当甲队清理完路面时,求乙队铺设完的路面长.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点A坐标为(-1,0).则下面的四个结论:①2a+b=0;②4a+2b+c>0 ③B点坐标为(4,0);④当x<-1时,y>0.其中正确的是
A.①② B.③④ C.①④ D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com