
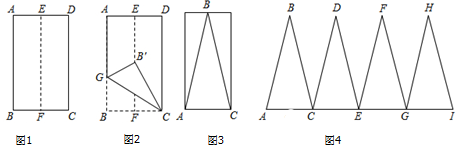
���� ��1�����ݾ��ε����ʺ��۵������ʵõ���BB'CΪ�ȱ������Σ��õ��𰸣�
��2���ֱ�ȡCE��EG��GI���е�P��Q��R������DP��FQ��HR��AD��AF��AH�����ݹ��ɶ������涨��֤����������Ϊֱ�������Σ����������ε������ʽ���㼴�ɣ�
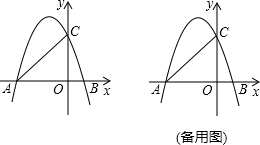
��� �⣺��1����ͼ2������BB'���������EF��ֱƽ��BC����BB'=B'C��
�ɷ��ۿɵã�B'C=BC��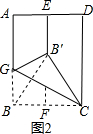
���BB'CΪ�ȱ������Σ�
���B'CB=60�㣬
���B'CG=30�㣬
���B'GC=60�㣻
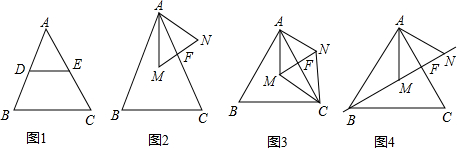
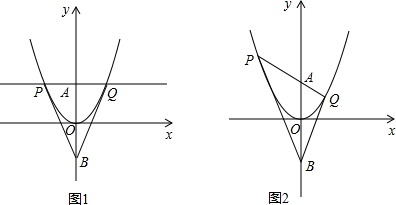
��2����ͼ4���ֱ�ȡCE��EG��GI���е�P��Q��R������DP��FQ��HR��AD��AF��AH��
�ߡ�ABC�У�BA=BC��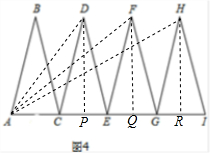
����ƽ�Ʊ任�����ʣ���CDE����EFG�͡�GHI���ǵ��������Σ�
��DP��CE��FQ��EG��HR��GI��
��Rt��AHR��AH=AI=4a��AH2=HR2+AR2��HR2=$\frac{15}{4}$a2��
��DP2=FQ2=HR2=$\frac{15}{4}$a2��
AD2=AP2+DP2=6a2��AF2=AQ2+FQ2=10a2��
�����������߳�Ϊ4a��$\sqrt{6}$a��$\sqrt{10}$a��
��AH2=AD2+AF2��
����������Ϊֱ�������Σ�
�����Ϊ$\frac{1}{2}$$\sqrt{6}$a��$\sqrt{10}$a=$\sqrt{15}$a2��
��$\sqrt{15}$a2��15$\sqrt{15}$��
��a2��15��
��a���������ֵΪ3��
���� ���⿼������۵������ʡ����ε����ʡ����������ε������Լ����ɶ������涨����Ӧ�ã����վ��ε����ʡ����������ε����ߺ�һ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 55�㣬55�� | B�� | 55�㣬70�� | ||
| C�� | 70�㣬40�� | D�� | 55�㣬55���70�㣬40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a•a2=a3 | B�� | 3a+2a2=5a2 | C�� | 2-3=-8 | D�� | $\sqrt{9}$=��3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com