
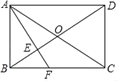
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,AF垂直平分OB,交OB于点E,若AB=6,则CF的长为_____.
【答案】4![]()
【解析】
由题意可证△ABO是等边三角形,可得∠BAO=60°,∠BAF=∠CAF=30°,由直角三角形的性质和等腰三角形性质可得BC=![]() AB=6
AB=6![]() ,AF=FC,由勾股定理可求FC的长.
,AF=FC,由勾股定理可求FC的长.
解:∵四边形ABCD是矩形
∴AO=BO=CO=DO,∠ABC=90°
∵AF垂直平分OB,
∴AB=AO,BE=EO,AF⊥BO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠BAO=60°,∠BAF=∠CAF=30°
∴∠ACB=90°﹣∠BAO=30°
∴∠FAC=∠ACF=30°,BC=![]() AB=6
AB=6![]() ,
,
∴AF=FC,
在Rt△ABF中,AF2=BF2+AB2,
∴CF2=(6![]() ﹣CF)2+36
﹣CF)2+36
∴CF=4![]() .
.
故答案是:4![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
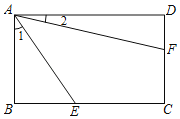
【题目】如图,矩形ABCD长与宽的比为5:3,点E、F分别在边BC、CD上,tan∠1=![]() ,tan∠2=
,tan∠2=![]() ,则cos(∠1+∠2)的值为( )
,则cos(∠1+∠2)的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
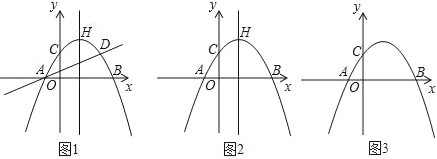
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A(﹣1,0)和B(3,0),与y轴交于C点,点C关于抛物线的对称轴的对称点为点D.抛物线顶点为H.
x2+bx+c与x轴交于A(﹣1,0)和B(3,0),与y轴交于C点,点C关于抛物线的对称轴的对称点为点D.抛物线顶点为H.
(1)求抛物线的解析式.
(2)当点E在抛物线的对称轴上运动时,在直线AD上是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在以动点Q,使PQ+![]() QB最小,若存在,请直接写出此时点Q的坐标及PQ+
QB最小,若存在,请直接写出此时点Q的坐标及PQ+![]() QB的最小值.
QB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为3的正三角形ABC放置在直线l上(AB与直线l重合),将正三角形ABC沿直线l向右做无滑动的滚动,正三角形ABC的任意一边与直线l重合时记录滚动次数,例如,正三角形ABC由图中位置①滚动到位置②时记录为滚动一次,当正三角形ABC由图中位置①开始滚动2018次时,点A经过的路径总长度为( )

A.2690πB.2692πC.4034πD.4036π
查看答案和解析>>
科目:初中数学 来源: 题型:
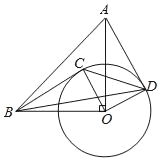
【题目】如图,在Rt△OAB中,∠AOB=90°,OA=OB=4,以点O为圆心、2为半径画圆,点C是⊙O上任意一点,连接BC,OC.将OC绕点O按顺时针方向旋转90°,交⊙O于点D,连接AD.
(1)当AD与⊙O相切时,
①求证:BC是⊙O的切线;
②求点C到OB的距离.
(2)连接BD,CD,当△BCD的面积最大时,点B到CD的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
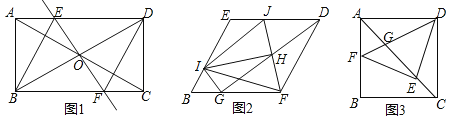
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面内一个⊙O半径为4,圆上有两个动点A、B,以AB为边在圆内作一个正方形ABDC,则OD的最小值是( )
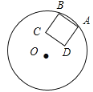
A.2B.![]() C.2
C.2![]() ﹣2D.4
﹣2D.4![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
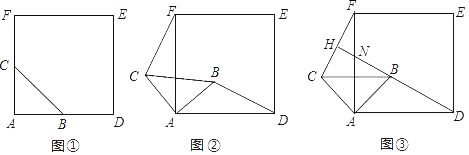
(1)当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(ⅰ)求证:BD⊥CF;
(ⅱ)当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com