
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:将点A、B坐标代入抛物线解析式,得:
![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为:y=﹣x2+4x+5
(2)
解:∵点P的横坐标为m,
∴P(m,﹣m2+4m+5),E(m,﹣ ![]() m+3),F(m,0).
m+3),F(m,0).
∴PE=|yP﹣yE|=|(﹣m2+4m+5)﹣(﹣ ![]() m+3)|=|﹣m2+
m+3)|=|﹣m2+ ![]() m+2|,
m+2|,
EF=|yE﹣yF|=|(﹣ ![]() m+3)﹣0|=|﹣
m+3)﹣0|=|﹣ ![]() m+3|.
m+3|.
由题意,PE=5EF,即:|﹣m2+ ![]() m+2|=5|﹣
m+2|=5|﹣ ![]() m+3|=|
m+3|=| ![]() m+15|
m+15|
①若﹣m2+ ![]() m+2=
m+2= ![]() m+15,整理得:2m2﹣17m+26=0,
m+15,整理得:2m2﹣17m+26=0,
解得:m=2或m= ![]() ;
;
②若﹣m2+ ![]() m+2=﹣(
m+2=﹣( ![]() m+15),整理得:m2﹣m﹣17=0,
m+15),整理得:m2﹣m﹣17=0,
解得:m= ![]() 或m=
或m= ![]() .
.
由题意,m的取值范围为:﹣1<m<5,故m= ![]() 、m=
、m= ![]() 这两个解均舍去.
这两个解均舍去.
∴m=2或m= ![]()
(3)
解:假设存在.
作出示意图如下:

∵点E、E′关于直线PC对称,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y轴,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四边形PECE′是菱形.
当四边形PECE′是菱形存在时,
由直线CD解析式y=﹣ ![]() x+3,可得OD=4,OC=3,由勾股定理得CD=5.
x+3,可得OD=4,OC=3,由勾股定理得CD=5.
过点E作EM∥x轴,交y轴于点M,易得△CEM∽△CDO,
∴ ![]() ,即
,即 ![]() ,解得CE=
,解得CE= ![]() |m|,
|m|,
∴PE=CE= ![]() |m|,又由(2)可知:PE=|﹣m2+
|m|,又由(2)可知:PE=|﹣m2+ ![]() m+2|
m+2|
∴|﹣m2+ ![]() m+2|=
m+2|= ![]() |m|.
|m|.
①若﹣m2+ ![]() m+2=
m+2= ![]() m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣
m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣ ![]() ;
;
②若﹣m2+ ![]() m+2=﹣
m+2=﹣ ![]() m,整理得:m2﹣6m﹣2=0,解得m1=3+
m,整理得:m2﹣6m﹣2=0,解得m1=3+ ![]() ,m2=3﹣
,m2=3﹣ ![]() .
.
由题意,m的取值范围为:﹣1<m<5,故m=3+ ![]() 这个解舍去.
这个解舍去.
当四边形PECE′是菱形这一条件不存在时,
此时P点横坐标为0,E,C,E'三点重合与y轴上,也符合题意,
∴P(0,5)
综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)
方法二:
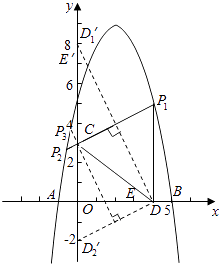
若E(不与C重合时)关于直线PC的对称点E′在y轴上,则直线CD与直线CE′关于PC轴对称.
∴点D关于直线PC的对称点D′也在y轴上,
∴DD′⊥CP,∵y=﹣ ![]() x+3,
x+3,
∴D(4,0),CD=5,
∵OC=3,
∴OD′=8或OD′=2,
①当OD′=8时,D′(0,8),设P(t,﹣t2+4t+5),D(4,0),C(0,3),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() ,
,
∴2t2﹣7t﹣4=0,
∴t1=4,t2=﹣ ![]() ,
,
②当OD′=2时,D′(0,﹣2),
设P(t,﹣t2+4t+5),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() =﹣1,
=﹣1,
∴t1=3+ ![]() ,t2=3﹣
,t2=3﹣ ![]() ,
,
∵点P是x轴上方的抛物线上一动点,
∴﹣1<t<5,
∴点P的坐标为(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3).
﹣3).
若点E与C重合时,P(0,5)也符合题意.
综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)
【解析】(1)利用待定系数法求出抛物线的解析式;(2)用含m的代数式分别表示出PE、EF,然后列方程求解;(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到点P坐标.


科目:初中数学 来源: 题型:
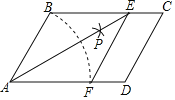
【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
求证:四边形ABEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )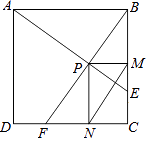
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
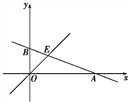
【题目】如图,已知函数y=-![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=-![]() x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(庆阳中考)现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了了解学生的视力变化情况,从全市九年级随机抽取了1 500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
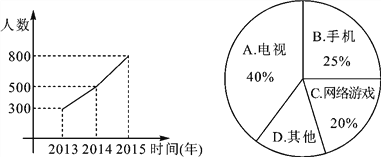
解答下列问题:
(1)图中D所在扇形的圆心角度数为______;
(2)若2016年全市共有30 000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°. 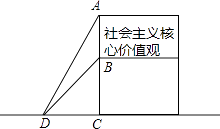
(1)求公益广告牌的高度AB;
(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com