
| 13 |
| 16 |
| 49 |
| 16 |
| 13 |
| 16 |
| 49 |
| 16 |
 水柱落地处刚好在最外轨道上,求当r为多少时,水池中安装的喷水龙头的个数最多?
水柱落地处刚好在最外轨道上,求当r为多少时,水池中安装的喷水龙头的个数最多?| 49 |
| 16 |
| 49 |
| 16 |
| 13 |
| 16 |
| 13 |
| 16 |
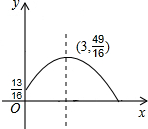 解:(1)如图,依题意建立平面直角坐标系,
解:(1)如图,依题意建立平面直角坐标系,| 49 |
| 16 |
| 13 |
| 16 |
| 13 |
| 16 |
| 49 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 49 |
| 16 |
| 1 |
| 4 |
| 49 |
| 16 |
| 1 |
| 2 |
| 13 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
| 13 |
| 2 |
| 2πr |
| 1.2 |
| 6.5-r |
| 1 |
| 5 |
| 3 |
| 5 |
| 3 |
| 13 |
| 4 |
| 845 |
| 48 |
| 13 |
| 4 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com