
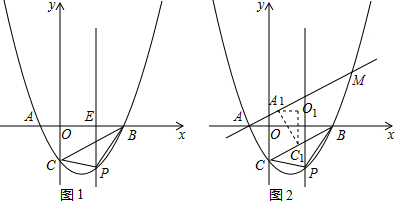
���� ��1�����ۣ���ABC��ֱ�������Σ���Rt��AOC�У���tan��ACO=$\frac{OA}{OC}$=$\frac{\sqrt{3}}{3}$���Ƴ���ACO=30�㣬��Rt��OBC�У���tan��BCO=$\frac{OB}{OC}$=$\sqrt{3}$���Ƴ���BCO=60�㣬�ɵá�ACB=��ACO+��BCO=90�㣻
��2����P��m��$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$����������CN��ʹ�á�BCN=60�㣬��FH��CN��H��FG��AE��G����FH=CF•cos30��=$\frac{\sqrt{3}}{2}$CF�����������P���꣬����G���˶�ʱ��=$\frac{EF}{1}$+$\frac{CF}{\frac{2\sqrt{3}}{3}}$=EF+$\frac{\sqrt{3}}{2}$CF=EF+FH�����ݴ��߶���̿�֪����EH��CNʱ������G���˶�ʱ����С���ɴ˼��ɽ�����⣻
��3�����ֱ��AM�Ľ���ʽ�����÷����������M���꣬������C�䣨t��$\frac{\sqrt{3}}{3}$t-$\sqrt{3}$�����������������ۣ���취�г����̼��ɽ�����⣻
��� �⣺��1�����ۣ���ABC��ֱ�������Σ�
���ɣ���ͼ1�У�����AC��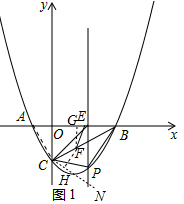
��������y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C��
��A��-1��0����B��3��0����C��0��-$\sqrt{3}$����
��Rt��AOC����tan��ACO=$\frac{OA}{OC}$=$\frac{\sqrt{3}}{3}$��
���ACO=30�㣬
��Rt��OBC����tan��BCO=$\frac{OB}{OC}$=$\sqrt{3}$��
���BCO=60�㣬
���ACB=��ACO+��BCO=90�㣬
���ABC��ֱ�������Σ�
��2����P��m��$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$����������CN��ʹ�á�BCN=60�㣬��FH��CN��H��FG��AE��G��
��FH=CF•cos30��=$\frac{\sqrt{3}}{2}$CF��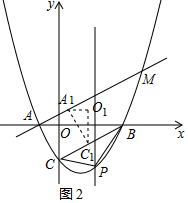
��S��PBC=S��POC+S��POB-S��BOC
=$\frac{1}{2}$��$\sqrt{3}$��m+$\frac{1}{2}$��3����-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$��-$\frac{1}{2}$��$\sqrt{3}$��3
=-$\frac{\sqrt{3}}{2}$��m-$\frac{3}{2}$��2+$\frac{9\sqrt{3}}{8}$��
��-$\frac{\sqrt{3}}{2}$��0��
��m=$\frac{3}{2}$ʱ����PBC��������ʱP��$\frac{3}{2}$��-$\frac{5\sqrt{3}}{4}$����
�߶���G���˶�ʱ��=$\frac{EF}{1}$+$\frac{CF}{\frac{2\sqrt{3}}{3}}$=EF+$\frac{\sqrt{3}}{2}$CF=EF+FH��
���ݴ��߶���̿�֪����EH��CNʱ������G���˶�ʱ����С��
�ߡ�EFB=��EBF=30�㣬
��EF=EB=$\frac{3}{2}$��
��Rt��EFG�У�FG=EF•cos30��=$\frac{3\sqrt{3}}{4}$��EG=$\frac{3}{4}$��OG=$\frac{3}{4}$��
���ʱF������Ϊ��$\frac{3}{4}$��-$\frac{3\sqrt{3}}{4}$����
��3��������ֱ��BC�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$��ֱ��AC�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$��
��$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}}\\{y=\frac{\sqrt{3}}{3}{x}^{2}-\frac{2\sqrt{3}}{3}x-\sqrt{3}}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=4}\\{y=\frac{5\sqrt{3}}{3}}\end{array}\right.$��
��M��4��$\frac{5\sqrt{3}}{3}$����
��C1��t��$\frac{\sqrt{3}}{3}$t-$\sqrt{3}$����
��AM2=52+��$\frac{5\sqrt{3}}{3}$��2��C1A2=��t+1��2+��$\frac{\sqrt{3}}{3}$t-$\sqrt{3}$��2��MC1=��4-t��2+��$\frac{5\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$��2��
�ٵ�AM=MC1ʱ��52+��$\frac{5\sqrt{3}}{3}$��2=��4-t��2+��$\frac{5\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$��2�����t=5+$\sqrt{22}$��5-$\sqrt{22}$��
�ڵ�C1A=C1Mʱ����t+1��2+��$\frac{\sqrt{3}}{3}$t-$\sqrt{3}$��2=��4-t��2+��$\frac{5\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$��2�����t=$\frac{5}{2}$
�۵�C1A=AMʱ��52+��$\frac{5\sqrt{3}}{3}$��2=��t+1��2+��$\frac{\sqrt{3}}{3}$t-$\sqrt{3}$��2�����t=$\sqrt{22}$s��-$\sqrt{22}$����������
��������������������t��ֵΪ��5+$\sqrt{22}$��s��5-$\sqrt{22}$��s��$\frac{5}{2}$s��$\sqrt{22}$s��
���� ���⿼����κ����ۺ��⡢������Ǻ�����һ�κ��������ʡ����������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����̽�����⣬�����п�ѹ���⣮


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
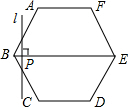 ��ͼ����������ABCDEF�ı߳�Ϊ6cm��P�ǶԽ���BE��һ���㣬����P��ֱ��l��BE��ֱ������P��B���������1cm/s���ٶ�����ƽ����E�㣮��ֱ��lɨ����������ABCDEF��������ΪS��cm2������P���˶�ʱ��Ϊt��s���������ܷ�ӳS��t֮�亯����ϵ�Ĵ���ͼ���ǣ�������
��ͼ����������ABCDEF�ı߳�Ϊ6cm��P�ǶԽ���BE��һ���㣬����P��ֱ��l��BE��ֱ������P��B���������1cm/s���ٶ�����ƽ����E�㣮��ֱ��lɨ����������ABCDEF��������ΪS��cm2������P���˶�ʱ��Ϊt��s���������ܷ�ӳS��t֮�亯����ϵ�Ĵ���ͼ���ǣ�������| A�� | 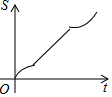 | B�� |  | C�� | 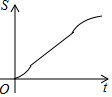 | D�� | 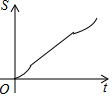 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
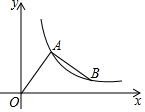 ��ͼ����ƽ��ֱ������ϵ�У���A��2��m���ǵ�һ������һ�㣬����OA����OA�Ƶ�A��ʱ����ת90��õ��߶�AB��������������y=$\frac{k}{x}$��x��0����ͼ��ǡ��ͬʱ������A��B����k��ֵΪ2+2$\sqrt{5}$��
��ͼ����ƽ��ֱ������ϵ�У���A��2��m���ǵ�һ������һ�㣬����OA����OA�Ƶ�A��ʱ����ת90��õ��߶�AB��������������y=$\frac{k}{x}$��x��0����ͼ��ǡ��ͬʱ������A��B����k��ֵΪ2+2$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
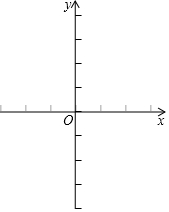 ������L��y=a��x-x1����x-x2��������a��0����x�ύ�ڵ�A��x1��0����B��x2��0������y�ύ�ڵ�C����x1•x2��0��AB=4����ֱ��l��y=-3x+t+2������t��0��ͬʱ������A��Cʱ��t=1��
������L��y=a��x-x1����x-x2��������a��0����x�ύ�ڵ�A��x1��0����B��x2��0������y�ύ�ڵ�C����x1•x2��0��AB=4����ֱ��l��y=-3x+t+2������t��0��ͬʱ������A��Cʱ��t=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
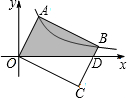 ��ͼ����ֱ������ϵ�У�����OABC�Ķ���A��B��˫����y=$\frac{k}{x}$�� x��0���ϣ�BC��x�ύ�ڵ�D������A������Ϊ��2��4�������D������Ϊ��������
��ͼ����ֱ������ϵ�У�����OABC�Ķ���A��B��˫����y=$\frac{k}{x}$�� x��0���ϣ�BC��x�ύ�ڵ�D������A������Ϊ��2��4�������D������Ϊ��������| A�� | ��$\frac{22}{3}$��0�� | B�� | ��$\frac{15}{2}$��0�� | C�� | ��$\frac{68}{9}$��0�� | D�� | ��$\frac{48}{5}$��0�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com