
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
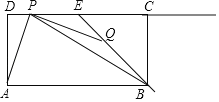
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
【答案】(1)①见解析;②S△PBQ=18﹣9![]() ;(2)存在,满足条件的t的值为6﹣3
;(2)存在,满足条件的t的值为6﹣3![]() 或3
或3![]() 或6+3
或6+3![]() .
.
【解析】
(1)①如图1中,过点Q作QF⊥CD于点F,证明Rt△ADP≌Rt△PFQ即可.
②如图,过点A作PB的垂线,垂足为H,过点Q作PB的垂线,垂足为G.由Rt△ADP≌Rt△AHP,推出PH=PD=t,AH=AD=3.由Rt△AHP△Rt△PGQ,推出QG=PH=DP=t,在Rt△AHB中,则有32+(6﹣t)2=62,求出t即可解决问题.
(2)分三种情形:①如图3﹣1中,若点P在线段DE上,当PQ=QB时.②如图3﹣2中,若点P在线段EC上(如图),当PB=BQ时.③如图3﹣3中,若点P在线段DC延长线上,QP=QB时,分别求解即可.
(1)①证明:如图1中,过点Q作QF⊥CD于点F,

∵点E是DC的中点,
∴CE=DE=3=CB,
又∵∠C=90°,
∴∠CEB=∠CBE=45°,
∵EQ=![]() t,DP=t,
t,DP=t,
∴EF=FQ=t.
∴FQ=DP,
∴PF=PE+EF=PE+DP=DE=3
∴PF=AD,
∴Rt△ADP≌Rt△PFQ,
∴AP=PQ.
②如图,过点A作PB的垂线,垂足为H,过点Q作PB的垂线,垂足为G.

由AP平分∠DPB,得∠APD=∠APB,易证Rt△ADP≌Rt△AHP,
∴PH=PD=t,AH=AD=3.
又∠APD=∠PAB,∴∠PAB=∠APB,
∴PB=AB=8,
易证Rt△AHP△Rt△PGQ,
∴QG=PH=DP=t,
在Rt△AHB中,则有32+(6﹣t)2=62,
解得t=6﹣3![]() ,
,
∴S△PBQ=![]() PBQG=
PBQG=![]() ×6×(6﹣3
×6×(6﹣3![]() )=18﹣9
)=18﹣9![]() .
.
(3)①如图3﹣1中,若点P在线段DE上,当PQ=QB时,
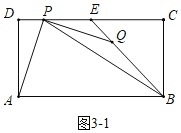
∴AP=PQ=QB=BE﹣EQ=3![]() ﹣
﹣![]() t,
t,
在Rt△APD中,由DP2+AD2=AP2,得t2+9=2(3﹣t)2,
解得t=6﹣3![]() 或6+3
或6+3![]() (舍去)
(舍去)
②如图3﹣2中,若点P在线段EC上(如图),当PB=BQ时,
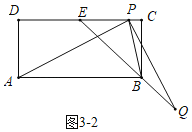
∴PB=BQ=![]() t﹣3
t﹣3![]() ,
,
则在Rt△BCP中,由BP2=CP2+BC2,得2(t﹣3)2=(6﹣t)2+9,
解得:t=3![]() 或
或 ![]() (舍去)
(舍去)
③如图3﹣3中,若点P在线段DC延长线上,QP=QB时,

∴AP=PQ=BQ=![]() t﹣3
t﹣3![]() ,
,
在Rt△APD中,由DP2+AD2=AP2,
得t2+9=2(t﹣3)2,解得![]() (舍去)或
(舍去)或![]()
综上所述,满足条件的t的值为6﹣3![]() 或3
或3![]() 或6+3
或6+3![]() .
.


科目:初中数学 来源: 题型:
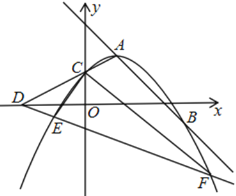
【题目】如图,抛物线y=![]() x2+mx+m(m>0)的顶点为A,交y轴于点C.
x2+mx+m(m>0)的顶点为A,交y轴于点C.
(1)求出点A的坐标(用含m的式子表示);
(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;
(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=(x﹣1)(x﹣2)(x﹣3)的图象与性质.小东对函数y=(x﹣1)(x﹣2)(x﹣3)的图象与性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=(x﹣1)(x﹣2)(x﹣3)的自变量x的取值范围是_______;
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | m | ﹣24 | ﹣6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
①m=_____;
②若M(﹣7,﹣720),N(n,720)为该函数图象上的两点,则n=_____;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,﹣yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x﹣1)(x﹣2)(x﹣3)(0≤x≤4)的图象.
③写出直线y=![]() x﹣1与②中你画出图象的交点的横坐标之和为______.
x﹣1与②中你画出图象的交点的横坐标之和为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
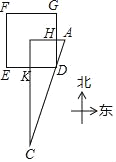
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为多少步.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因2019年下半年猪肉大涨,某养猪专业户想扩大养猪场地,但为了节省材料,利用一面墙(墙足够长)为一边,用总长为120![]() 的材料围成了如图所示①②③三块矩形区域,而且这三块矩形区域的面积相等,设
的材料围成了如图所示①②③三块矩形区域,而且这三块矩形区域的面积相等,设![]() 的长度为
的长度为![]() (
(![]() ),矩形区域
),矩形区域![]() 的面积
的面积![]() (
(![]() ).
).

(1)求![]() 与
与![]() 之间的函数表达式,并注明自变量
之间的函数表达式,并注明自变量![]() 的取值范围.
的取值范围.
(2)当![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线 y = x与反比例函数![]() 的图象交于点A(2,m).
的图象交于点A(2,m).

(1)求m和k的值;
(2)点P(xP,yP)是函数![]() 图象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
图象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
①当yP = 4时,求线段BP的长;
②当BP![]() 3时,结合函数图象,直接写出点P 的纵坐标yP的取值范围.
3时,结合函数图象,直接写出点P 的纵坐标yP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:函数y=﹣x2+mx+2m(m为常数)的图象不经过第二象限,当﹣5≤x≤1时,函数的最大值与最小值之差为12.25,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
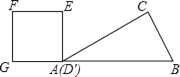
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2![]() 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com