
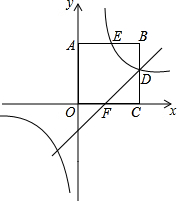
 已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.
已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.分析 (1)由正方形的性质及点A的坐标得出OC=3,求出x=3时y2的值得出点D的坐标,继而得出反比例函数的解析式;
(2)根据直线和双曲线的解析式求得OF=1、AE=2,从而求得S四边形AOFE=$\frac{9}{2}$,设点P(x,x-1),得出S△POF=$\frac{1}{2}$×1×|x-1|=$\frac{9}{2}$,解之求得x的值,从而求得点P的坐标.
解答 解:(1)∵四边形OABC是正方形,且点A坐标为(0,3),
∴OA=OC=3,
将x=3代入y2=x-1,得:y2=2,
∴点D的坐标为(3,2),
则反比例函数的表达式为y1=$\frac{6}{x}$;
(2)将y=0代入y2=x-1得:x=1,
∴OF=1,
将y=3代入y1=$\frac{6}{x}$,得:x=2,
∴AE=2,
则S四边形AOFE=$\frac{1}{2}$×(1+2)×3=$\frac{9}{2}$,
设点P的坐标为(x,x-1),
则S△POF=$\frac{1}{2}$×1×|x-1|=$\frac{9}{2}$,
解得:x=10或x=-8,
当x=10时,y=9;当x=-8时,y=-9,
∴点P的坐标为(10,9)或(-9,-8).
点评 本题主要考查直线与双曲线的交点问题,熟练掌握待定系数法求函数的解析式及三角形的面积问题是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源:2017届广西马山县民族中学春季学期第一次月考八年级数学试卷(解析版) 题型:单选题
以下运算正确的是( )
A. 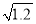 是最简二次根式;
是最简二次根式;
B. 三边长分别为4、5、6的三角形是直角三角形;
C. 直角三角形两直角边的和等于斜边的长;
D. 等腰直角三角形腰长为1,则斜边长为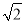 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题:
一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
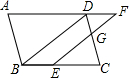 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )| A. | $\frac{25a}{8}$ | B. | $\frac{25a}{9}$ | C. | $\frac{25a}{16}$ | D. | $\frac{16a}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
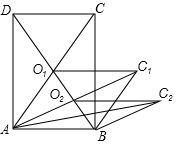 如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.
如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com