
 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )| A. | ∠3+∠4=180° | B. | ∠2+∠5>180° | C. | ∠1+∠6<180° | D. | ∠2+∠7=180° |
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
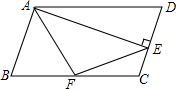 已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )
已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )| A. | ①②④ | B. | ①③ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
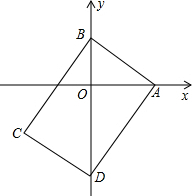 如图,在矩形ABCD中,AB=3,AD=4,顶点A、B、D在坐标轴上.将矩形ABCD平移,使点C与原点O重合,则平移后点A的对应点A′的坐标为(4.8,1.4).
如图,在矩形ABCD中,AB=3,AD=4,顶点A、B、D在坐标轴上.将矩形ABCD平移,使点C与原点O重合,则平移后点A的对应点A′的坐标为(4.8,1.4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com