Question

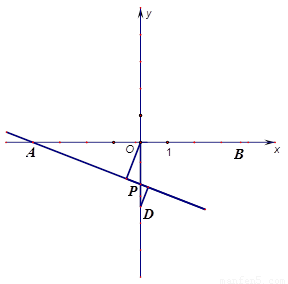
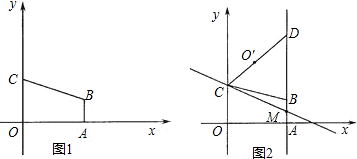
如图1：直线y= kx+4k（k≠0）交x轴于点A，交y轴于点C，点M(2，m)为直线AC上一点，过点M的直线BD交x轴于点B，交y轴于点D．

(1)求的值（用含有k的式子表示．）；

(2)若SBOM =3SDOM，且k为方程(k+7)(k+5)-(k+6)(k+5=的根，求直线BD的解析式．

(3)如图2，在(2)的条件下，P为线段OD之间的动点（点P不与点O和点D重合），OE

上AP于E，，DF上AP于F，下列两个结论：①值不变；②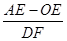值不变，请你判断其中哪一个结论是正确的，并说明理由并求出其值，

 

Answer 1

【答案】

 

（1）

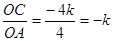
（2）

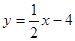
（3）

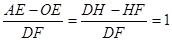
【解析】（1）解：∵A（-4,0）  C(0,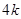)                             ……2分

       由图象可知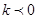

∴OA=4 ,  OC=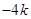                                              ……3分

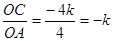∴                                              ……4分

（2）解： ∵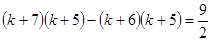

          解得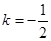：                                             ……5分

∴直线AC的解析式为：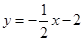

∴M（2，-3）                                                   ……6分

过点M作M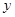E⊥轴于E

∴ME=2

∵

∴

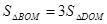
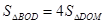
     又∵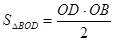   

     ∴

     ∴                                               

∴

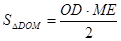
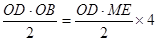
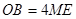
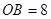
     ∴B（8，0）                                                   ……7分    

     设直线BD的解析式为：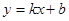

     则有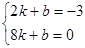         

解得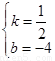：……9分

     ∴直线BD的解析式为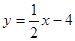：                             ……8分

（3）解：②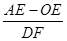值不变.理由如下：

过点O作OH⊥DF交DF的延长线于H，连接EH                       ……9分

∵DF⊥AP

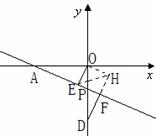∴∠DFP=∠AOP=90º

又∠DPF=∠APO

∴∠ODH=∠OAE

∵点D在直线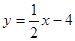

∴D(0，-4)

∴OA=OD=4

又∵∠OHD=∠OEA=90 º

∴△ODH≌⊿OAE（AAS）                                           ……10分

∴AE=DH ，  OE=OH ， ∠HOD=∠EOA

∴∠EOH=∠HOD+∠EOD=∠EOA+∠EOD=90º                          ……11分

∴∠OEH=45º

∴∠HEF=45º=∠FHE

∴FE=FH

∴等腰Rt⊿OH≌等腰Rt⊿FHE

∴OE=OH=FE=HF

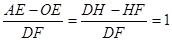∴                                       ……12分