
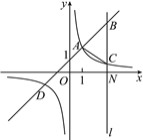
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,2),D(-2,-1).直线l⊥x轴,与x轴交于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2),D(-2,-1).直线l⊥x轴,与x轴交于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的表达式;
(2)求△ABC的面积;
(3)根据图象回答:当x在什么范围时,一次函数的值大于反比例函数的值.
【答案】(1) y=x+1,![]() ;(2) S△ABC=
;(2) S△ABC=![]() ;(3)-2<x<0或x>1.
;(3)-2<x<0或x>1.
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)首先求得B和C的坐标,则BC的长即可求得,然后利用三角形的面积公式求解;
(3)求一次函数的值大于反比例函数时x的范围就是求一次函数的图象在反比例函数的图象的上边部分对应的自变量x的范围.
(1)把(1,2)代入y=![]() ,得m=2,则反比例函数的表达式是y=
,得m=2,则反比例函数的表达式是y=![]() .
.
根据题意,得![]() 解得
解得![]()
则一次函数的表达式是y=x+1.
(2)在y=![]() 中,令x=3得y=
中,令x=3得y=![]() ,则点C的坐标是(3,
,则点C的坐标是(3,![]() ).
).
在y=x+1中,令x=3,则y=4,则点B的坐标是(3,4).
则BC=4-![]() =
=![]() ,
,
则S△ABC=![]() ×
×![]() ×(3-1)=
×(3-1)=![]() .
.
(3)-2<x<0或x>1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
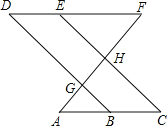
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若![]() ,
,![]() .
.
求证:![]() .
.
证明:![]()
![]() ______
______![]() 对顶角相等
对顶角相等![]()
![]() ,
,
![]() ______
______![]()
![]() ______
______![]() ______
______![]()
又![]()
![]() ,
,
![]() ______
______![]() ______
______![]()
![]() ______
______![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为 . 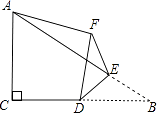
查看答案和解析>>
科目:初中数学 来源: 题型:
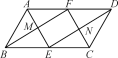
【题目】如图,ABCD中,∠ABC=60°,AB=4,AD=8,点E,F分别是边BC,AD的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△AˊBD.
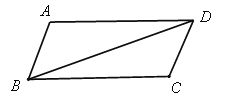
(1)利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法);
(2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三张形状、大小均相同但画面不同的风景图片都按同样的方式剪成相同的两片,然后堆放到一起混合洗匀,背面朝上,从这堆图片中随机抽出两张,这两张图片恰好能组成一张原风景图片的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC. 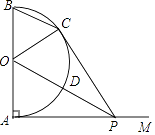
(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空: ①当AP=时,四边形OAPC是正方形;
②当AP=时,四边形BODC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是一个无理数筛选器的工作流程图.
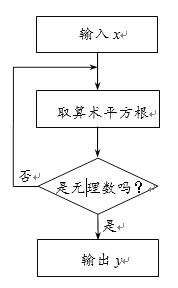
(1)当![]() 为16时,
为16时,![]() 值为 ;
值为 ;
(2)是否存在输入有意义的![]() 值后,却始终输不出
值后,却始终输不出![]() 值?如果存在,写出所有满足要求的
值?如果存在,写出所有满足要求的![]() 值;如果不存在,请说明理由;
值;如果不存在,请说明理由;
(3)如果输入![]() 值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的
值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的![]() 值可能是什么情况;
值可能是什么情况;
(4)当输出的![]() 值是
值是![]() 时,判断输入的
时,判断输入的![]() 值是否唯一,如果不唯一,请写出其中的两个.
值是否唯一,如果不唯一,请写出其中的两个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com