试题分析:(1)先确定A的位置,再作出△AOB,就可以求出AB=2,OB=
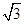
,在y轴上符合条件的有两点C1和C2,求出即可;
(2)根据AP=AO=1,得出P的对称点是O点,求出OC,即可得出OP,解直角三角形求出PQ和OQ即可;
(3)作出B关于y轴的对称点,连接PB′即可得出M点的位置,求出PB′长即可.
试题解析:(1)符合条件的有两点,以A为圆心,以AB为半径画弧,交y轴于C
1、C
2点,
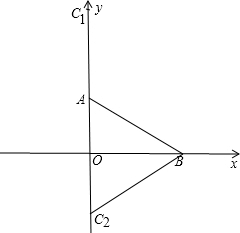
∵A(0,1),
∴OA=1,
∵在Rt△AOB中,OA=1,∠ABO=30°,
∴AB=2OA=2,OB=
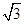
,
即AC
1=AC
2=2,
∴OC
1=1+2=3,OC
2=2-1=2,
∴C的坐标是(0,3)或(0,-1),
(2)P的坐标是(
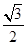
,
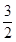
),
理由是:过P作PQ⊥x轴于Q,
∵OA=1,AP=1,AO⊥x轴,
∴x轴和以A为圆心,以1为半径的圆相切,
∵AP=1,
∴P在圆上,
∵点P关于直线AB的对称点P′在x轴上,AP=1,
∴P′点和O重合,如图:

∵P和P′关于直线AB对称,
∴PP′⊥AB,PC=P′C,
由三角形面积公式得:S
△AOB=
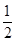
AO×OB=
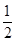
AB×CO,
∴
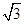
×1=2OC,
∴OC=
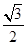
,
∴PP′=2OC=
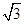
,
∵∠ABO=30°,∠OCB=90°,
∴∠POB=60°,
∴PQ=OP×sin60°=
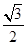
,OQ=OP×cos60°=
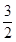
,
即P的坐标是(
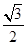
,
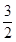
);
(3)作B关于y轴的对称点B′,连接PB′交y轴于M,则M为所求,
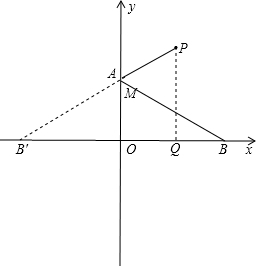
∵OB=
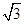
,
∴OB′=
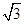
,
即BB′=2
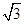
,
∵PQ=
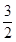
,
∴由勾股定理得:PB′=
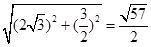
,
∴PM+BM=PM+B′M=PB′=
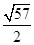
.
考点: 1.轴对称-最短路线问题;2.坐标与图形性质;3.等腰三角形的性质.


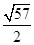 .
.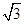 ,在y轴上符合条件的有两点C1和C2,求出即可;
,在y轴上符合条件的有两点C1和C2,求出即可;
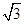 ,
,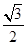 ,
,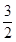 ),
),
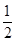 AO×OB=
AO×OB=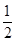 AB×CO,
AB×CO,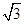 ×1=2OC,
×1=2OC,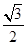 ,
,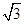 ,
,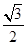 ,OQ=OP×cos60°=
,OQ=OP×cos60°=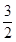 ,
,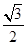 ,
,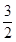 );
);
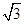 ,
,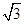 ,
,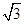 ,
,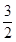 ,
,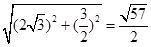 ,
,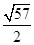 .
.
