
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).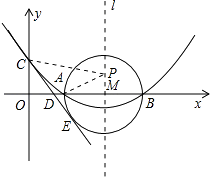
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
【答案】
(1)
解:由题意,设抛物线的解析式为y=a(x﹣4)2﹣ ![]() (a≠0)
(a≠0)
∵抛物线经过(0,2)
∴a(0﹣4)2﹣ ![]() =2
=2
解得:a= ![]()
∴y= ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]()
即:y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
当y=0时, ![]() x2﹣
x2﹣ ![]() x+2=0
x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0)
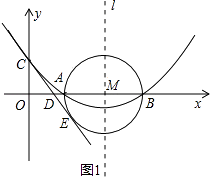
(2)
解:存在,
如图2,由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2 ![]() ,
,
∴AP+CP=BC=2 ![]()
∴AP+CP的最小值为2 ![]()
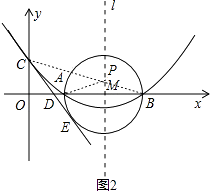
(3)
解:如图3,连接ME
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
∵C的坐标(0,2),
∴OC=2,
∵AB=4,
∴ME=2
∴OC=ME=2,
∵∠ODC=∠MDE,
∵在△COD与△MED中
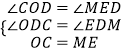
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
则CD=DM=OM﹣OD=4﹣x
则Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4﹣x)2
∴x= ![]()
∴D( ![]() ,0)
,0)
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D( ![]() ,0)两点,
,0)两点,
则 
解得: 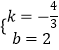
∴直线CE的解析式为y=﹣ ![]() +2;
+2;

【解析】(1)利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标;(2)线段BC的长即为AP+CP的最小值;(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x,在RT△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E. 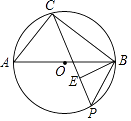
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有( ) 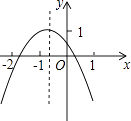
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过对角线BD上一点P,作EF∥BC,HG∥AB,若四边形AEPH和四边形CFPG的面积分另为S1和S2,则S1与S2的大小关系为( )
A.S1=S2 B.S1>S2 C.S1<S2 D.不能确定

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )
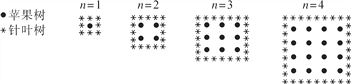
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数1个1,2个![]() ,3个
,3个![]() ,…,n个
,…,n个![]() (n为正整数)顺次排成一列:1,
(n为正整数)顺次排成一列:1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,记a1=1,a2=
,…,记a1=1,a2=![]() ,a3=
,a3=![]() ,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位) 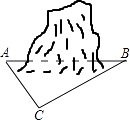
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于点C,O是坐标原点,已知点B的坐标是(3,0),tan∠OAC=3;
(1)求该抛物线的函数表达式;
(2)点P在x轴上方的抛物线上,且∠PAB=∠CAB,求点P的坐标;
(3)若平行于x轴的直线与抛物线交于点M、N(M点在N点左侧),
①若以MN为直径的圆与x轴相切,求该圆的半径;
②若Q(m,4)是直线MN上一动点,当以点C、B、Q为顶点的三角形的面积等于6时,请直接写出符合条件的m值,为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com