
 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.求证:四边形AECG是平行四边形.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.求证:四边形AECG是平行四边形.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
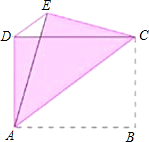 如图,ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠.点B落在E处,连接DE.四边形ACED是什么图形?为什么?它的面积是多少?周长呢?
如图,ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠.点B落在E处,连接DE.四边形ACED是什么图形?为什么?它的面积是多少?周长呢?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,ABCD是矩形纸片,翻折∠B、∠D使BC边、AD边恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
如图,ABCD是矩形纸片,翻折∠B、∠D使BC边、AD边恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2009•郑州模拟)如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(2009•郑州模拟)如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com