
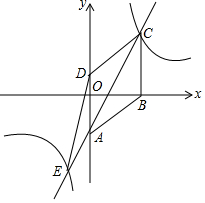
 已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b.
已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b.分析 (1)先求得C得坐标,然后根据待定系数法即可求得;
(2)求得直线的解析式,然后联立方程,解方程组求得交点坐标,根据图象即可求得;
(3)根据S△CDE=S△ADE+S△ADC求得即可.
解答 解:(1)∵A(0,-3),B(4,0),
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5=BC,
∴C(4,5),
∵反比例函数y1=$\frac{k}{x}$图象经过点C,
∴k=4×5=20,
∴反比例函数解析式为y1=$\frac{20}{x}$;
(2)把A(0,-3),C(4,5)代入y2=ax+b得,
$\left\{\begin{array}{l}{b=-3}\\{4a+b=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$
直线AC解析式为y2=2x-3,
解$\left\{\begin{array}{l}{y=2x-3}\\{y=\frac{20}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\frac{5}{2}}\\{{y}_{2}=-8}\end{array}\right.$,
∴E(-$\frac{5}{2}$,-8)
当当y1<y2时,x>4或-$\frac{5}{2}$<x<0;
(3)S△CDE=S△ADE+S△ADC=$\frac{1}{2}$××$5×\frac{5}{2}$+$\frac{1}{2}$×5×4=$\frac{65}{4}$.
点评 本题考查了菱形的性质,待定系数法求一次函数和反比例函数的解析式,一次函数和反比例函数的交点等,求得C点的坐标是解题的关键.


科目:初中数学 来源: 题型:选择题
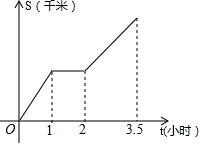 星期天,小明从家出发,以15千米/小时的速度骑车去郊游,到达目的地休息一段时间后原路返回,已知小明行驶的路程s(千米)与时间t(小时)之间的函数关系如图所示,则小明返程的速度为( )
星期天,小明从家出发,以15千米/小时的速度骑车去郊游,到达目的地休息一段时间后原路返回,已知小明行驶的路程s(千米)与时间t(小时)之间的函数关系如图所示,则小明返程的速度为( )| A. | 15千米/小时 | B. | 10千米/小时 | C. | 6千米/小时 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
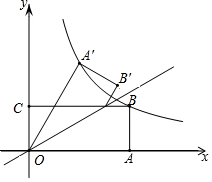 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.
如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
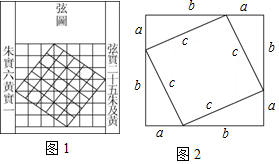 中国数学史上有许多著名的数学家,很多理论都是由他们的名字命名的.如图1就是著名的“赵爽弦图”,它是由公元3世纪三国时期的赵爽为证明某个定理而创设的一副“弦图”,图2由“弦图”变化得到,请用含a,b,c的等式表示定理的内容a2+b2=c2.
中国数学史上有许多著名的数学家,很多理论都是由他们的名字命名的.如图1就是著名的“赵爽弦图”,它是由公元3世纪三国时期的赵爽为证明某个定理而创设的一副“弦图”,图2由“弦图”变化得到,请用含a,b,c的等式表示定理的内容a2+b2=c2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a-2a=a | B. | $\sqrt{2}+\sqrt{5}$=$\sqrt{7}$ | C. | (2a)3=2a3 | D. | a6÷a3=a2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com