练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
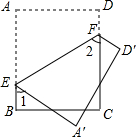
    4．如图，E、F分别是矩形ABCD边AB、CD上的点，将矩形ABCD沿EF折叠，使A、D分别落在A′和D′处，若∠1=50°，则∠2的度数是（　　）
    A．65°B．60°C．50°D．40°

    分析 由折叠的性质得到∠AEF=∠A′EF，根据平行线的性质即可得到结论．

    解答 解：由折叠的性质得，∠AEF=∠A′EF，
    ∵∠1=50′，
    ∴∠AEF=∠A′EF=$\frac{180°-∠1}{2}$=65°，
    ∵四边形ABCD是矩形，
    ∴AB∥CD，
    ∴∠2=∠AEF=65°，
    故选A．

    点评 本题考查了翻折变换-折叠问题，矩形的性质，平行线的性质，熟练掌握折叠的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．已知a、b、c满足a2+2b=7，b2-2c=-1，c2-6a=-17，则a+b+c=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

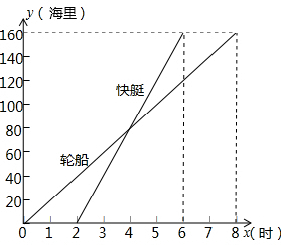    15．已知A、B两个海港相距180海里．如图表示一艘轮船和一艘快艇沿相同路线从A港出发到B港航行过程中路程随时间变化的图象（分别是正比例函数图象和一次函数图象）．通过计算解答下列问题：
    （1）请分别求出表示轮船和快艇行驶过程的函数表达式（不要求写出自变量的取值范围）；
    （2）快艇出发多长时间后能超过轮船？
    （3）快艇和轮船哪一艘先到达B港？早到多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，直线l1∥l2∥l3，直线AC分别交l1、l2、l3于点A、B、C，直线DF分别交l1、l2、l3于点D、E、F，AC与DF相交于点H，则下列式子不正确的是（　　）
    A．$\frac{AB}{BC}$=$\frac{DE}{EF}$B．$\frac{AB}{DE}$=$\frac{BC}{EF}$C．$\frac{AB}{AC}$=$\frac{DE}{DF}$D．$\frac{AB}{BC}$=$\frac{BE}{CF}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知关于x的方程x2-（m+2）x+2m-1=0．
    （1）求证：此方程有两个不相等的实数根；
    （2）若抛物线y=x2-（m+2）x+2m-1=0与x轴有两个交点都在x轴正半轴上，求m的取值范围；
    （3）填空：若x2-（m+2）x+2m-1=0的两根都大于1，则m的取值范围是m＞2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，AC、BD相交于点O，且OA=OC=4，OB=OD=6，P是线段BD上一动点，过点P作EF∥AC，与四边形的两条边分别交于点E，F，设BP=x，EF=y，则下列能表示y与x之间函数关系的图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（$\sqrt{3}$，1）在反比例函数y=$\frac{k}{x}$（x≠0）的图象上．
    （1）求反比例函数y=$\frac{k}{x}$（x≠0）的解析式和点B的坐标；
    （2）若将△BOA绕点B按逆时针方向旋转60°得到△BDE（点O与点D是对应点），补全图形，直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．新房装修后，甲居民购买家居用品的清单如下表，因污水导致部分信息无法识别，根据下表解决问题：
    家居用品名称单价（元）数量（个）金额（元）
    挂钟30260
    垃圾桶15
    塑料鞋架40
    艺术字画a290
    电热水壶351b
    合计8280
    （1）直接写出a=45，b=35；
    （2）甲居民购买了垃圾桶，塑料鞋架各几个？
    （3）若甲居民再次购买艺术字画和垃圾桶两种家居用品，共花费150元，则有哪几种不同的购买方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

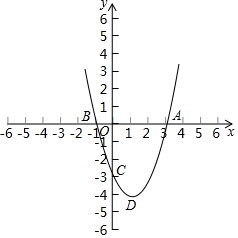    14．如图，在平面直角坐标系中，二次函数y=x2+bx+c的对称轴为经过点（1，0）的直线，其图象与x轴交于点A、B，且过点C（0，-3），其顶点为D．
    （1）求这个二次函数的解析式及顶点坐标；
    （2）在y轴上找一点P（点P与点C不重合），使得∠APD=90°，求点P的坐标；
    （3）在（2）的条件下，将△APD沿直线AD翻折得到△AQD，求点Q的坐标．

    查看答案和解析>>

    同步练习册答案