
【题目】如图,四边形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半抽上,点
轴的正半抽上,点![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿线段
个单位长度的速度沿线段![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线
的垂线![]() 交线段
交线段![]() 于点
于点![]() ,以线段
,以线段![]() 为斜边向右作等腰直角
为斜边向右作等腰直角![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1) 点F的坐标为( , )点![]() 的坐标为( , )(用含
的坐标为( , )(用含![]() 的代数式表示),
的代数式表示),
(2)连接![]() 、
、![]() ,当
,当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)设点![]() 从点
从点![]() 出发时,点
出发时,点![]() 、
、![]() 、
、![]() 都与点
都与点![]() 重合,点
重合,点![]() 在运动过程中,当
在运动过程中,当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 运动的时间
运动的时间![]() 的值﹒
的值﹒
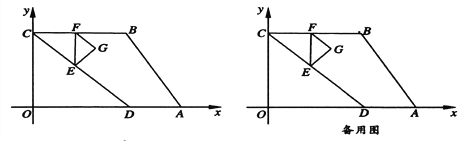
【答案】(1) G(![]() ); (2) t=2或t=
); (2) t=2或t=![]() -2;(3)见解析.
-2;(3)见解析.
【解析】
根据等腰直角三角形的性质和勾股定理,求出CF=EF=t,然后表示出F点的坐标,再根据直角三角形斜边上的中线等于斜边的一半,求出G的坐标;
(2)根据相似三角形的对应边相等,分类讨论求出t的值即可;
(3)求出直线AB的解析式,过点G作x轴的平行线交AB于点H,根据点G的坐标求出H的坐标,根据三角形的面积求解即可.
(1)∵OC=OD=4
∴∠OCD=45°
∵CE=![]() t,
t,
∴CF=FE=t
∴F点为(t,4)
∵△EFG是等腰直角三角形,
∴G点到y轴的距离为![]() t
t
即G(![]() );
);
(2) ∵CE=![]() , ∴EF=CF=t,FG=
, ∴EF=CF=t,FG=![]() ,BF=4-t, ∵∠OCE=∠BFG=45°, ①若△OCE∽△BFG,则
,BF=4-t, ∵∠OCE=∠BFG=45°, ①若△OCE∽△BFG,则![]() ,即
,即![]() ,解得t=2; ②若△ECO∽BFG,则
,解得t=2; ②若△ECO∽BFG,则![]() ,即
,即 ![]() ,解得t=
,解得t=![]() -2;综上所述,当t=2或t=
-2;综上所述,当t=2或t=![]() -2时,以C 、E 、O 为顶点的三角形与 相似.
-2时,以C 、E 、O 为顶点的三角形与 相似.
(3)设直线AB的方程为y=kx+b,则![]() ,解得
,解得![]() ,∴y=-2x+12,
,∴y=-2x+12,

过点G作x轴的平行线交AB于点H, ∵点G的坐标为(![]() ),将y=4-
),将y=4-![]() 代入y=-2x+12得x=4+
代入y=-2x+12得x=4+![]() ,∴点H的坐标为(
,∴点H的坐标为(![]() ),
),![]() ,由2
,由2![]() ,得t=
,得t=![]() 或t=
或t=![]() (舍去).
(舍去).


科目:初中数学 来源: 题型:
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的周长为
的周长为![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,点
两点同时出发,点![]() 以
以![]() 的速度按顺时针方向在三角形的边上运动,点
的速度按顺时针方向在三角形的边上运动,点![]() 以
以![]() 的速度按逆时针方向在三角形的边上运动.设
的速度按逆时针方向在三角形的边上运动.设![]() ,
,![]() 两点第一次在三角形
两点第一次在三角形![]() 的顶点处相遇的时间为
的顶点处相遇的时间为![]() ,第二次在三角形
,第二次在三角形![]() 顶点处相遇的时间为
顶点处相遇的时间为![]() ,则
,则![]() _______.
_______.
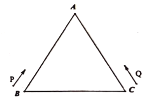
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 和点
和点![]() 在数轴上对应的数分别为
在数轴上对应的数分别为![]() 和
和![]() ,且
,且![]() .
.
(1)线段![]() 的长为 ;
的长为 ;
(2)点![]() 在数轴上所对应的数为
在数轴上所对应的数为![]() ,且
,且![]() 是方程
是方程![]() 的解,在线段
的解,在线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ?若存在,请求出点
?若存在,请求出点![]() 在数轴上所对应的数,若不存在,请说明理由;
在数轴上所对应的数,若不存在,请说明理由;
(3)在(2)的条件下,线段![]() 和
和![]() 分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为
分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为![]() 秒,点
秒,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,若
的中点,若![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的几个式子:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;…
;…
(1)根据上面的规律,第5个式子为:________________.
(2)根据上面的规律,第n个式子为:________________.
(3)利用你发现的规律,写出![]() …
…![]() ________________.
________________.
(4)利用你发现的规律,求出![]() …
…![]() 的值,并写出过程。
的值,并写出过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.
(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,求2017年该地至少有多少户享受到优先搬迁租房奖励.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com