
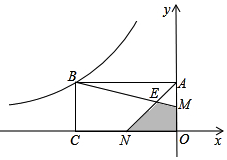
 如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )| A. | y=-$\frac{10}{x}$ | B. | y=-$\frac{8}{x}$ | C. | y=-$\frac{6}{x}$ | D. | y=-$\frac{4}{x}$ |
分析 过M作MG∥ON,交AN于G,过E作EF⊥AB于F,由题意可知:AM=OM=a,ON=NC=2a,AB=OC=4a,BC=AO=2a,再根据三角形相似以及三角形面积之间的关系求出B点坐标,即双曲线解析式求出.
解答 解:过M作MG∥ON,交AN于G,过E作EF⊥AB于F,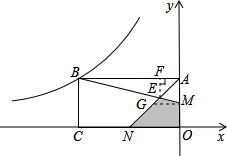
设EF=h,OM=a,
由题意可知:AM=OM=a,ON=NC=2a,AB=OC=4a,BC=AO=2a
△AON中,MG∥ON,AM=OM,
∴MG=$\frac{1}{2}$ON=a,
∵MG∥AB
∴$\frac{MG}{AB}$=$\frac{ME}{BE}$=$\frac{1}{4}$,
∴BE=4EM,
∵EF⊥AB,
∴EF∥AM,
∴$\frac{FE}{AM}$=$\frac{BE}{BM}$=$\frac{4}{5}$.
∴FE=$\frac{4}{5}$AM,即h=$\frac{4}{5}$a,
∵S△ABM=4a×a÷2=2a2,
S△AON=2a×2a÷2=2a2,
∴S△ABM=S△AON,
∴S△AEB=S四边形EMON=2,
S△AEB=AB×EF÷2=4a×h÷2=2,
ah=1,又有h=$\frac{4}{5}$a,a=$\frac{\sqrt{5}}{2}$(长度为正数)
∴OA=$\sqrt{5}$,OC=2$\sqrt{5}$,
因此B的坐标为(-2$\sqrt{5}$,$\sqrt{5}$),
经过B的双曲线的解析式就是y=-$\frac{10}{x}$.
点评 本题主要考查反比例函数的综合题的知识,解答本题的关键是辅助线的作法和相似三角形的性质的应用,此题难度中等.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 240人 | B. | 360人 | C. | 380人 | D. | 420人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8x9÷4x3=2x6 | B. | 4a2b3÷4a2b3=0 | C. | a2m÷am=a2 | D. | 2a2b÷(-$\frac{1}{2}$ab2)=-4c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
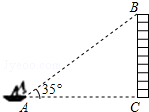 如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为59m.(精确到1m)
如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为59m.(精确到1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com