
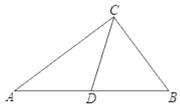
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D为AB的中点,将△ACD绕着点C逆时针旋转,使点A落在射线CB的上A′处,点D落在点D′处,
(1)请依题意画出图形;
(2)求D′B长为 .
【答案】(1)见解析;(2)![]()
【解析】
(1)依题意画出图形即可;
(2)根据勾股定理可得AB=5,根据中点的性质可得CD=AD=BD=![]() AB=2.5,再根据勾股定理可得D′E=
AB=2.5,再根据勾股定理可得D′E=![]() =1.5,根据A′E=CE=2,BC=3,可得BE=1,再根据勾股定理即可求出D′B的值.
=1.5,根据A′E=CE=2,BC=3,可得BE=1,再根据勾股定理即可求出D′B的值.
解:(1)如图所示:

(2)∵在Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=5,
∵点D为AB的中点,
∴CD=AD=BD=![]() AB=2.5,
AB=2.5,
过D′作D′E⊥BC,
∵将△ACD绕着点C逆时针旋转,使点A落在CB的延长线A′处,点D落在点D′处,
∴CD′=AD=A′D′,
∴D′E=![]() =1.5,
=1.5,
∵A′E=CE=2,BC=3,
∴BE=1,
∴BD′=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】电影公司随机收集了2000部电影的有关数据,经分类整理得到如表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 |
|
|
|
|
|
|
注:好评率是指一类电影中获得好评的部数与该类电影的部数的比值.
![]() 如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
![]() 电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化
电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化![]() 假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加
假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加![]() ,哪类电影的好评率减少
,哪类电影的好评率减少![]() ,可使改变投资策略后总的好评率达到最大?
,可使改变投资策略后总的好评率达到最大?
答:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OC是⊙O的半径,点D是半圆AB上一动点(不与A、B重合),连结DC交直径AB与点E,若∠AOC=60°,则∠AED的范围为( )
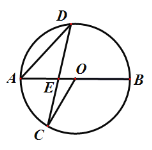
A.0°< ∠AED <180°B.30°< ∠AED <120°
C.60°< ∠AED <120°D.60°< ∠AED <150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.

(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
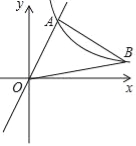
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为 .
,∠AOB=∠OBA=45°,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
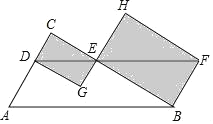
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,BA=5,点D是边AC上的一动点,过点D作DE∥AB交边BC于点E,过点B作BF⊥BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,AD的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
①经过三个点一定可以作圆;②若等腰三角形的两边长分别为3和7,则第三边长是3或7;③一个正六边形的内角和是其外角和的2倍;④随意翻到一本书的某页,页码是偶数是随机事件;⑤关于x的一元二次方程x2-(k+3)x+k=0有两个不相等的实数根.
A.①②③B.①④⑤C.②③④D.③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com