
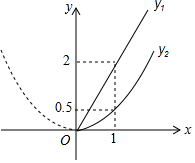
 随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)
随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)分析 (1)设y1=kx(k≠0),根据图形可知点(1,2)在正比例函数图象上,利用待定系数法即可求出y1关于投入资金x的函数关系式;由抛物线的顶点为原点可设y2=ax2(a≠0),结合图形中抛物线上的点(1,0.5)利用待定系数法即可求出y2关于投入资金x的函数关系式;
(2)设这个专业户投入种植花卉x万元(0≤x≤10),则投入种植树木(10-x)万元,他获得的利润是z万元,根据总利润=种植花卉利润+种植树木利润,即可得出z关于x的二次函数关系式,根据二次函数的性质即可解决最值问题,此题得解.
解答 解:(1)设y1=kx(k≠0),
由图可知,函数y1=kx的图象过点(1,2),
∴2=k×1,k=2,
∴y1关于投入资金x的函数关系式为y1=2x.
∵抛物线的顶点为原点,
∴设y2=ax2(a≠0),
由图可知,函数y2=ax2的图象过点(1,0.5),
∴0.5=a×12,a=$\frac{1}{2}$.
∴y2关于投入资金x的函数关系式为y2=$\frac{1}{2}$x2.
(2)设这个专业户投入种植花卉x万元(0≤x≤10),则投入种植树木(10-x)万元,他获得的利润是z万元,
根据题意得:z=2(10-x)+$\frac{1}{2}$x2=$\frac{1}{2}$x2-2x+20=$\frac{1}{2}$(x-2)2+18,
当x=2时,z取最小值18,
∵0≤x≤10,
∴-2≤x-2≤8,
∴(x-2)2≤64.
∴$\frac{1}{2}$(x-2)2≤32,
∴$\frac{1}{2}$(x-2)2+18≤32+18=50,即z≤50,
当z=50时,x=10,
故10万元全部用来投资种植花卉时,可获得最大利润,最大利润为50万元.
点评 本题考查了二次函数的应用、待定系数法求函数解析式以及二次函数的性质,根据图形中点的坐标利用待定系数法求出函数解析式是解题的关键.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是5cm.
如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
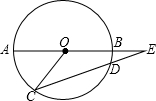 如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
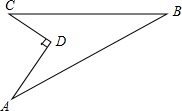 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
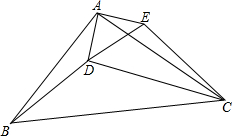 如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由.
如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com