
阅读理解
我们知道:多项式a2+6a+9可以写成(a+3)2的形式,这就是将多项式a2+6a+9因式分解.当一个多项式(如a2+6a+8)不能写成两数和(或差)的平方的形式时,我们通常采用下面的方法:
a2+6a+8=(a+3)2﹣1=(a+2)(a+4).
请仿照上面的方法,将下列各式因式分解:
(1)x2﹣6x﹣27;(2)a2+3a﹣28;(3)x2﹣(2n+1)x+n2+n.
(1)(x+3)(x﹣9) (2)(a﹣4)(a+7) (3)(x﹣n﹣1)(x﹣n)
解析试题分析:根据题目的条件,先将多项式凑成完全平方的形式,再根据实际情况解答.
解:(1)x2﹣6x﹣27,
=x2﹣6x+9﹣36,
=(x﹣3)2﹣62,
=(x﹣3﹣6)(x﹣3+6),
=(x+3)(x﹣9);
(2)a2+3a﹣28,
=a2+3a+(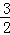 )2﹣(
)2﹣(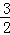 )2﹣28,
)2﹣28,
=(a+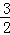 )2﹣
)2﹣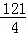 ,
,
=(a+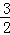 ﹣
﹣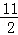 )(a+
)(a+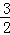 +
+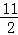 ),
),
=(a﹣4)(a+7);
(3)x2﹣(2n+1)x+n2+n,
=x2﹣(2n+1)x+(n+ )2﹣(n+
)2﹣(n+ )2+n2+n,
)2+n2+n,
=(x﹣n﹣ )2﹣(
)2﹣( )2,
)2,
=(x﹣n﹣ ﹣
﹣ )(x﹣n
)(x﹣n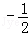 +
+ ),
),
=(x﹣n﹣1)(x﹣n).
考点:因式分解-运用公式法.
点评:本题考查了公式法分解因式,是信息给予题,主要渗透配方思想,读懂题目信息是解题的关键.


科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com