
【题目】已知二次函数y=﹣2x2+bx+c的图象经过点A(0,4)和B(1,﹣2).
(1)求此抛物线的解析式;
(2)求此抛物线的对称轴和顶点坐标;
(3)设抛物线的顶点为C,试求△CAO的面积.
【答案】(1)y=﹣2x2﹣4x+4;(2)对称轴为直线x=﹣1,顶点坐标为(﹣1,6);(3)△CAO的面积为2.
【解析】
(1)利用待定系数法把A(0,4)和B(1,﹣2)代入y=﹣2x2+bx+c中,可以解得b,c的值,从而求得函数关系式即可;
(2)利用配方法求出图象的对称轴和顶点坐标;
(3)由(2)可得顶点C的坐标,再根据三角形的面积公式即可求出△CAO的面积.
解:(1)把A(0,4)和B(1,﹣2)代入y=﹣2x2+bx+c,
得:![]() ,解得:
,解得:![]() ,
,
所以此抛物线的解析式为y=﹣2x2﹣4x+4;
(2)∵y=﹣2x2﹣4x+4
=﹣2(x2+2x)+4
=﹣2[(x+1)2﹣1]+4
=﹣2(x+1)2+6,
∴此抛物线的对称轴为直线x=﹣1,顶点坐标为(﹣1,6);
(3)由(2)知:顶点C(﹣1,6),
∵点A(0,4),∴OA=4,
∴S△CAO=![]() OA|xc|=
OA|xc|=![]() ×4×1=2,
×4×1=2,
即△CAO的面积为2.
故答案为:(1)y=﹣2x2﹣4x+4;(2)对称轴为直线x=﹣1,顶点坐标为(﹣1,6);(3)△CAO的面积为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
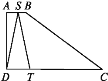
【题目】如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=1,AD=3,DC=5.点S沿A→B→C运动到C点停止,以S为圆心,SD为半径作弧交射线DC于T点,设S点运动的路径长为x,等腰△DST的面积为y,则y与x的函数图象应为( )
A. 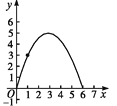 B.
B. 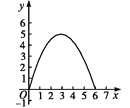
C. 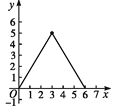 D.
D. 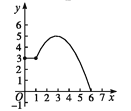
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A,点B(﹣1,0),与y轴交于点C(0,4),作直线AC.
(1)求抛物线解析式;
(2)点P在抛物线的对称轴上,且到直线AC和x轴的距离相等,设点P的纵坐标为m,求m的值;
(3)点M在y轴上且位于点C上方,点N在直线AC上,点Q为第一象限内抛物线上一点,若以点C、M、N、Q为顶点的四边形是菱形,请直接写出点Q的坐标.
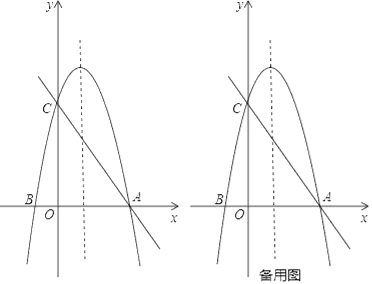
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明设计用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=18米,那么该古城墙的高度是( )
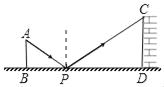
A. 6米 B. 8米 C. 12米 D. 24米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取点A,过点A作AH⊥x轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P、O、Q为顶点,且以点Q为直角顶点的三角形与△AOH全等,则符合条件的点A的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线![]() ,且经过点A(3,-1),与y轴交于点B.
,且经过点A(3,-1),与y轴交于点B.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若![]() ,试求出点P的坐标.
,试求出点P的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com