
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×![]() ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .

(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少?
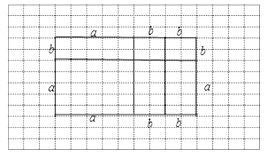
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
【答案】(1)详见解析;(2) ![]() ;(3)详见解析>
;(3)详见解析>
【解析】
(1)梯形的面积可以由梯形的面积公式求出,也利用三个直角三角形面积求出,两次求出的面积相等列出关系式,化简即可得证;
(2)已知两直角边,利用勾股定理求出斜边长,再利用面积法即可求出斜边上的高.
(3)已知图形面积的表达式,即可根据表达式得出图形的边长的表达式,即可画出图形.
解:(1)梯形ABCD的面积为![]() (a+b)(a+b)=
(a+b)(a+b)=![]() a2+ab+
a2+ab+![]() b2 ,
b2 ,
也利用表示为![]() ab+
ab+![]() c2+ab,
c2+ab,
∴![]() a2+ab+
a2+ab+![]() b2=
b2=![]() ab+
ab+![]() c2+
c2+![]() ab,即a2+b2=c2
ab,即a2+b2=c2
(2)∵直角三角形的两直角边分别为3,4,
∴斜边为5,
∵设斜边上的高为h,直角三角形的面积为![]() ×3×4=
×3×4=![]() ×5×h,
×5×h,
∴h=![]() .
.
(3)∵图形面积为:(a+b)(a+2b)=a2+3ab+2b2 ,
∴边长为(a+2b)(a+b),
由此可画出的图形为:


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】合肥百货大厦某店卖一种狗宝宝布娃娃纪念品,已知成批购进时单价为4元,根据市场调查,销售量与销售单价在一段时间内满足如下关系:单价为10元时销售量为300枚,而单价每降低1元,就可多售出5枚,那么求可获得最大利润为__元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC≌△DEF,点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季即将来临,某电器超市销售每台进价分别为200元、170元的A,B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 2台 | 3台 | 1130元 |
第二周 | 5台 | 6台 | 2510元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)分别求出A,B两种型号电风扇的销售单价;
(2)若超市准备用不超过5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com