
| A. | 当AB=BC时,四边形ABCD是菱形 | B. | 当AC=BD时,四边形是正方形 | ||
| C. | 当∠ABC=90°时,四边形是矩形 | D. | 当AC⊥BD时,四边形是菱形 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
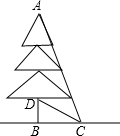 某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1)
某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
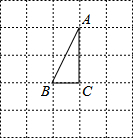 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.
如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com