
 已知:如图,∠1=∠2,∠3=∠4.求证:AC=AD.(用两种不同的判定方法)
已知:如图,∠1=∠2,∠3=∠4.求证:AC=AD.(用两种不同的判定方法) 分析 △ABD与△ABC有一条公共边AB,∠1=∠2,要证明△ABD≌△ABC,只需证∠ABD=∠ABC或∠D=∠C.
解答 解:方法一:
∵∠3=∠4(已知)
∴∠ABD=180°-∠3
∠ABC=180°-∠4(邻补角定义)
∴∠ABD=∠ABC(等角的补角相等)
在△ABD和△ABC中
$\left\{\begin{array}{l}{∠1=∠2(已知)}\\{AB=AB(公共边)}\\{∠ABC=∠ABD(已证)}\end{array}\right.$
△ABD≌△ABC(ASA)
∴AC=AD(全等三角形的对应边相等)
方法二:
∵∠3=∠4,∠1=∠2(已知)
∠3=∠1+∠D
∠4=∠2+∠C(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠D=∠C
在△ABD和△ABC中
$\left\{\begin{array}{l}{∠1=∠2(已知)}\\{∠D=∠C(已证)}\\{AB=AB(公共边)}\end{array}\right.$
∴△ABD≌△ABC(AAS)
∴AC=AD(全等三角形的对应边相等)
点评 本题考查的是全等三角形的判定和性质.证明线段相等通常证明线段所在的两个三角形全等.全等三角形的对应边相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
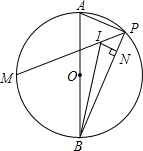 如图,AB为⊙O的直径,点M为半圆的中点,点P为另一半圆上一点(不与A、B重合),点I为△ABP的内心,IN⊥BP于N.
如图,AB为⊙O的直径,点M为半圆的中点,点P为另一半圆上一点(不与A、B重合),点I为△ABP的内心,IN⊥BP于N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是10本.
某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是10本.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com