

分析 (1)根据非负数的性质即可解决问题.
(2)如图1中,作PE∥OB于E,PF⊥AO于F,则四边形PEOF是正方形,将△PEB绕点P逆时针旋转90°得到△PFM.只要证明△APB≌△APM,推出AB=EB+AF,由此即可解决问题.
(3)如图3中,作NE⊥OM于E,HF⊥OM于F交OP于J,HG⊥x轴于G,设点H坐标(m,n).求出EN,FG,由△MNE∽△OHG,得到$\frac{MN}{OH}$=$\frac{EN}{GH}$,由此即可解决问题.
解答 解:(1)∵$\sqrt{m-n}$+(m-2)2=0,
$\sqrt{m-n}$≥0,(m-2)2≥0,
∴m=n=2,
∴点P坐标为(2,2).
(2)如图1中,作PE∥OB于E,PF⊥AO于F,则四边形PEOF是正方形,将△PEB绕点P逆时针旋转90°得到△PFM.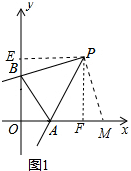
∵∠APB=45°,∠EPF=90°,
∴∠EPB+∠APF=∠APF+∠FPM=45°,
∴∠APB=∠APM,
在△APB和△APM中,
$\left\{\begin{array}{l}{PB=PM}\\{∠APB=∠APM}\\{PA=PA}\end{array}\right.$,
∴△APB≌△APM,
∴AB=AM=AF+FM=AF+EB,
∴△AOB的周长=OB+OA+AB=OB+OA+AF+EB=OE+OF=4.
(3)如图3中,作NE⊥OM于E,HF⊥OM于F交OP于J,HG⊥x轴于G,设点H坐标(m,n).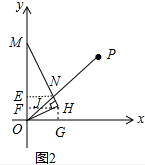
∵∠JOF=∠FJO=45°,'
∴OF=FJ=n,OJ=$\sqrt{2}$n,
∵∠FHO+∠FHM=90°,∠FMH+∠FHM=90°,
∴∠FHO=∠FMH=∠HOJ,
∴OJ=JH=$\sqrt{2}$n,
∵FH=OG,
∴m=n+$\sqrt{2}$n,
∴n=($\sqrt{2}$-1)n,
∵FH∥OG,
∴∠FHO=∠HOG,
∵∠HON=∠FHO,
∴∠NOH=∠HOG,
∵∠OHN=∠HGO=90°,
∴△OHN∽△OGH,
∴$\frac{ON}{OH}$=$\frac{OH}{OG}$,
∴ON=$\frac{{m}^{2}+(\sqrt{2}-1)^{2}{m}^{2}}{m}$=(4-2$\sqrt{2}$)m,
∵EN=$\frac{\sqrt{2}}{2}$ON,
∴EN=(2$\sqrt{2}$-2)m,
∵∠HOG=∠EMN,∠OGH=∠MEN=90°,
∴△MNE∽△OHG,
∴$\frac{MN}{OH}$=$\frac{EN}{GH}$=$\frac{(2\sqrt{2}-2)m}{(\sqrt{2}-1)m}$=2.
点评 本题考查三角形综合题、非负数的性质、全等三角形的判定和性质相似三角形的判定和性质等知识,解题的关键是相交添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考常考题型.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | (x+4)2=9 | B. | (x-4)2=9 | C. | (x-8)2=16 | D. | (x+8)2=57 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{k}{x}$在第一象限的图象过点A(1,3)和点C,点C与点A不重合,连结OA、OC,以OA、OC为边作?ABCO.
如图,已知反比例函数y=$\frac{k}{x}$在第一象限的图象过点A(1,3)和点C,点C与点A不重合,连结OA、OC,以OA、OC为边作?ABCO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 方差 | C. | 平 均数 | D. | 頻数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{4x+3y=2}\\{7x+5y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+3y=2}\\{23x+17y=11}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+4y=2}\\{7x+5y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+4y=2}\\{23x+17y=11}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com